《2025年新课程学习指导南方出版社八年级数学上册华师大版》

4. 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的大正方形(如图11所示). 如果大正方形的面积是13,小正方形的面积是1,直角三角形中较短的直角边为a,较长的直角边为b,那么$(a+b)^2$的值为(C)

A.13
B.19
C.25
D.169

答案： C

1. 如图12,一个边长为1丈的正方形池塘的正中间长有一根芦苇,高出水面1尺,有人将芦苇的尖端引到岸边,尖端刚好接触水面. 问：池塘有多深,芦苇有多高？(1丈= 10尺)

答案： 设池塘深度为$x$尺，则芦苇高为$(x + 1)$尺。
正方形池塘边长1丈=10尺，正中间到岸边距离为$\frac{10}{2}=5$尺。
由勾股定理得：$x^2 + 5^2=(x + 1)^2$
展开得：$x^2 + 25=x^2 + 2x + 1$
化简得：$25=2x + 1$
解得：$2x=24$，$x=12$
芦苇高：$x + 1=13$
答：池塘深12尺，芦苇高13尺。

2. 某宾馆在重新装修后考虑在大厅的主楼梯上铺设地毯,已知主楼梯梯宽3m,其剖面如图13所示,AB= 2.1m,AC= 3.5m,如果地毯每平方米40元,那么,仅此楼梯购买地毯的开支是多少元？

答案： 解：由题意，将楼梯水平方向的线段向上平移，竖直方向的线段向左平移，可得地毯的总长度为AB + BC。
在Rt△ABC中，AB=2.1m，AC=3.5m，根据勾股定理：
BC² = AC² - AB² = 3.5² - 2.1² = 12.25 - 4.41 = 7.84，
∴BC = √7.84 = 2.8m。
地毯总长度：AB + BC = 2.1 + 2.8 = 4.9m。
地毯面积：4.9×3 = 14.7m²。
购买地毯开支：14.7×40 = 588元。
答：仅此楼梯购买地毯的开支是588元。

3. 如图14,一个长方体盒子的盒内长、宽、高分别是30cm、24cm和18cm,盒内可放的棍子最长有多长？(提示：图中的阴影三角形是直角三角形)

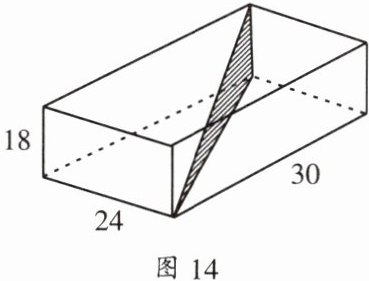
答案： 根据题意，长方体盒内对角线为可放棍子的最长长度。
设长方体盒内对角线长度为$l$，由勾股定理，在底面长方形中，底面对角线长度$d$为：
$d = \sqrt{30^{2} + 24^{2}} = \sqrt{900 + 576} = \sqrt{1476}=6\sqrt{41}(cm)$。
再考虑长方体的高，由勾股定理，盒内对角线$l$为：
$l = \sqrt{d^{2} + 18^{2}} = \sqrt{(6\sqrt{41})^{2} + 18^{2}} = \sqrt{1476 + 324} = \sqrt{1800} = 30\sqrt{2}(cm)$。
所以盒内可放的棍子最长长度为$30\sqrt{2}cm$。