《2025年课堂点睛七年级数学上册人教版安徽专版》

1. 某农村有耕地1000亩,分别种植粮食、棉花和蔬菜. 其中蔬菜用地$a$亩,粮食用地比蔬菜用地的6倍还多$b$亩.
(1)粮食用地多少亩？
(2)当$a = 120$,$b = 4$时,棉花用地多少亩？

答案：
(1)解:粮食用地$(6a+b)$亩；
(2)当$a=120,b=4$时,棉花用地为$1000-a-(6a+b)=1000-120-(6×120+4)=156$(亩).

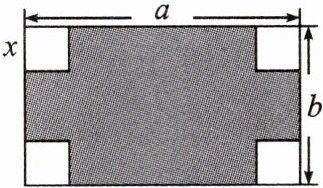
2. 如图,某长方形广场的四角都有一块边长为$x$米的正方形草地,若长方形广场的长为$a$米,宽为$b$米.
(1)请用代数式表示阴影部分的面积；
(2)若长方形广场的长为200米,宽为150米,正方形的边长为10米,求阴影部分的面积.

答案：
(1)解:阴影部分的面积为$(ab-4x^{2})$平方米.
(2)阴影部分的面积为$200×150-4×10^{2}=29600$(平方米).

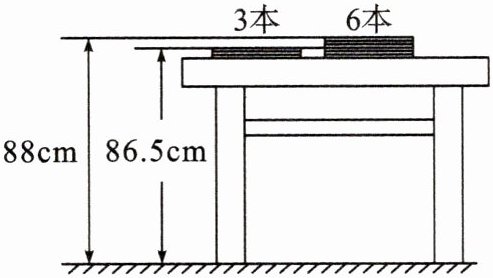
3. 如图,两摞规格完全相同的课本整齐地叠放在桌子上,请根据图中所给出的数据信息,回答下列问题：
(1)求每本课本的厚度；
(2)若有一摞上述规格的课本$x$本,整齐地叠放在桌子上,用含$x$的代数式表示出这一摞课本的顶部距离地面的高度；
(3)在(2)的条件下,当$x = 35$时,求课本的顶部距离地面的高度.

答案：
(1)解:$(88-86.5)÷(6-3)=0.5(cm)$,即每本课本的厚度为0.5cm；
(2)课桌的高度是:$86.5-0.5×3=85(cm)$,$x$本书的高度是:$0.5x$cm,即这摞课本的顶部距离地面的高度是:$(0.5x+85)cm$；
(3)当$x=35$时,$0.5x+85=0.5×35+85=102.5(cm)$,即课本的顶部距离地面的高度是102.5cm.

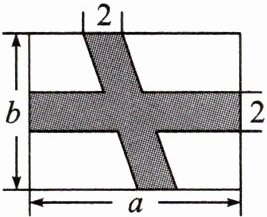
4. 如图是一个长为$a$,宽为$b$的长方形,两个涂色部分的图形都是底边长为2,且底边在长方形对边上的平行四边形.
(1)用含$a$,$b$的式子表示长方形中空白部分的面积；
(2)当$a = 8$,$b = 6$时,求长方形中空白部分的面积.

答案：
(1)解:$ab-2a-2b+2×2=ab-2a-2b+4$,即长方形中空白部分的面积为$ab-2a-2b+4$；
(2)当$a=8,b=6$时,$ab-2a-2b+4=8×6-2×8-2×6+4=48-16-12+4=24$,即长方形中空白部分的面积为24.