《2025年课堂点睛七年级数学上册人教版安徽专版》

12. 一个有理数和它的相反数的积是(C)
A.正数
B.负数
C.零或负数
D.零或正数

答案： C

13. 从有理数$\frac{1}{2}$,$0$,$1$,$-3$中任取两个数相乘,所得的积中最小的为(B)
A.$0$
B.$-3$
C.$-\frac{3}{2}$
D.$\frac{1}{2}$

答案： B

14. 如果$a + b ＞ 0$,且$ab ＞ 0$,那么(A)
A.$a ＞ 0$,$b ＞ 0$
B.$a$,$b$异号,且正数的绝对值较小
C.$a ＜ 0$,$b ＜ 0$
D.$a$,$b$异号,且负数的绝对值较小

答案： A

15. (分类讨论思想)若$|a| = 3$,$|b| = 4$,且$a ＞ b$,则$ab$的值为(A)

A.$\pm12$
B.$\pm1$
C.$1或-7$
D.$7或-1$
【变式】变条件
已知$|a| = 4$,$|b| = 2$. 且$ab ＞ 0$,则$a - b$的值为2 或-2.

答案： A
@@2 或-2

16. 计算：
(1)$1\frac{2}{3}×(-1\frac{1}{5})$；
(2)$(-3.25)×(-\frac{2}{13})$；
(3)$36×(-9\frac{11}{12})$.

答案：
(1)解:原式$=-\frac{5}{3}×\frac{6}{5}=-2$.
(2)解:原式$=-\frac{13}{4}×(-\frac{2}{13})=\frac{13}{4}×\frac{2}{13}=\frac{1}{2}$.
(3)解:原式$=36×(-\frac{119}{12})=-36×\frac{119}{12}=-357$.

17. (情境题)某超市现有20筐白菜,以每筐18千克为标准,超过和不足的千克数分别用正、负数来表示,记录如下：

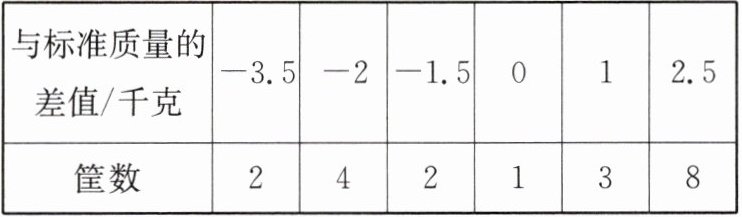
(1)这20筐白菜中,最重的一筐比最轻的一筐重6千克；
(2)与标准质量比较,这20筐白菜总计超过或不足多少千克？
解:$2×(-3.5)+4×(-2)+2×(-1.5)+1×0+3×1+8×2.5=5$(千克).所以与标准质量比较,这20筐白菜总计超过5千克.
(3)若该超市参与了“送温暖惠民工程”,白菜每千克的售价为1.8元,则出售这20筐白菜可卖多少元？
解:$1.8×(18×20+5)=1.8×365=657$(元).所以出售这20筐白菜可卖657元.

答案：
(1)6
(2)解:$2×(-3.5)+4×(-2)+2×(-1.5)+1×0+3×1+8×2.5=5$(千克).所以与标准质量比较,这20筐白菜总计超过5千克.
(3)$1.8×(18×20+5)=1.8×365=657$(元).所以出售这20筐白菜可卖657元.

18. (核心素养·推理能力)定义：$a$是不为1的有理数,我们把$\frac{1}{1 - a}称为a$的差倒数. 如：2的差倒数是$\frac{1}{1 - 2} = -1$；$-1的差倒数是\frac{1}{1 - (-1)} = \frac{1}{2}$. 已知$a_1 = -\frac{1}{3}$,$a_2是a_1$的差倒数,$a_3是a_2$的差倒数,$a_4是a_3$的差倒数,以此类推.
(1)求$a_2$,$a_3$,$a_4$的值；
(2)求$a_{2024}$的值.

答案：
(1)解:$a_{2}=\frac{3}{4},a_{3}=4,a_{4}=-\frac{1}{3}$.
(2)经计算,发现结果以$-\frac{1}{3},\frac{3}{4},4$三个数依次不断循环.因为$2024÷3=674\cdots\cdots2$,所以$a_{2024}=a_{2}=\frac{3}{4}$.