《2025年自主学习能力测评六年级数学上册人教版》

4 如图，正方形的边长是 6 cm，四个圆的圆心分别是正方形的四个顶点。涂色部分的面积是多少平方厘米？

答案： 4. $6÷2 = 3$（$cm$） $6×6 - 3.14×3^{2}=7.74$（$cm^{2}$）

5 距今约五千年前（新石器时代），位于辽宁牛河梁红山文化遗址的三环石坛（如图），有可能是中国最早的“天坛”，三个圆的直径从小到大分别是 11 m、15.6 m、22 m，构成了十分精确的比的关系，体现了“天圆地方”的象征意义。你能计算这个圜丘中的涂色部分面积吗？请你试一试。

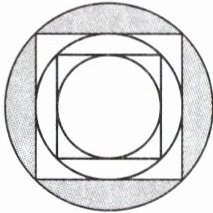
答案： 5. $22÷2 = 11$（$m$） $3.14×11^{2}=379.94$（$m^{2}$） $15.6×15.6 = 243.36$（$m^{2}$）
$379.94 - 243.36 = 136.58$（$m^{2}$）

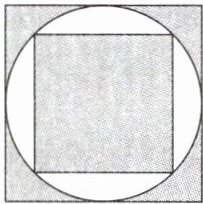
6 如图是我国一个古建筑的门窗图，方中有圆，圆中有方。已知大正方形的面积是$2dm^{2}$，小正方形的面积是(1)$dm^{2}$。

答案： 6. 1

7 小新用边长为 12 cm 的正方形纸设计了三种手抄报版式（如图），他打算将阴影部分涂上颜色，空白部分用来摘抄文字，这三种设计中涂色部分的面积相等吗？为什么？

答案： 7. 相等，因为涂色部分的面积都是正方形的面积减去一个直径是$12 cm$的圆的面积。