第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1 如图,已知圆的直径为 4 cm,在圆里画一个最大的正方形,剩余部分的面积是多少?
要求剩余部分的面积,就要知道正方形的面积,怎么求正方形的面积呢?

(1)可以把正方形看成两个(
(2)三角形的底 =(
(3)求三角形的面积,这样列式:
(4)求剩余部分的面积,列式:$S_{圆}-S_{正}=S_{圆}-2×S_{三角形}=$
自
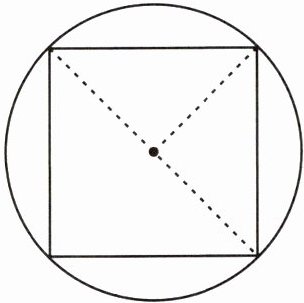
要求剩余部分的面积,就要知道正方形的面积,怎么求正方形的面积呢?

(1)可以把正方形看成两个(
三角形
)来求面积。(2)三角形的底 =(
4
)cm,三角形的高 =(2
)cm。(3)求三角形的面积,这样列式:
$4×2÷2 = 4$($cm^{2}$)
。(4)求剩余部分的面积,列式:$S_{圆}-S_{正}=S_{圆}-2×S_{三角形}=$
$3.14×(4÷2)^{2}-4×2$
=$4.56$
($cm^{2}$)。自
主
小
结 在“外圆内方”中,圆的直径 =(正方形的对角线
);在“外方内圆”中,圆的直径 =(正方形的边长
)。
答案:
1. (1)三角形 (2)4 2 (3)$4×2÷2 = 4$($cm^{2}$) (4)$3.14×(4÷2)^{2}-4×2 = 4.56$
正方形的对角线 正方形的边长
正方形的对角线 正方形的边长
2 算一算,填一填。
如图,在正方形内画一个最大的圆,如果圆的面积是$314cm^{2}$,那么正方形的面积是(
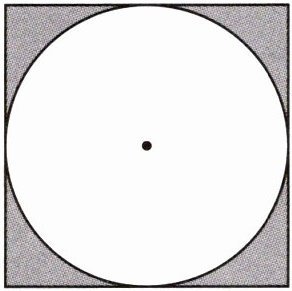
你有什么发现?
如图,在正方形内画一个最大的圆,如果圆的面积是$314cm^{2}$,那么正方形的面积是(
400
)$cm^{2}$,圆和正方形的面积之比是$3.14:$(4
)。如果圆的面积是$12.56cm^{2}$,那么正方形的面积是(16
)$cm^{2}$,圆和正方形的面积之比是$3.14:$(4
)。
你有什么发现?
在正方形里画一个最大的圆,圆和正方形的面积之比是$3.14:4$(答案不唯一)
。
答案:
2. 400 4
16 4 在正方形里画一个最大的圆,圆和正方形的面积之比是$3.14:4$(答案不唯一)
16 4 在正方形里画一个最大的圆,圆和正方形的面积之比是$3.14:4$(答案不唯一)
3 “风流天子出崇观,铁画银钩字字端。闻道蜀中铜货少,任凭顽铁买江山。”这首诗传述的便是北宋徽宗皇帝所创的书法“瘦金体”,北宋货币“大观通宝”是由徽宗御题钱文,因此被称为御书钱。一枚“大观通宝”钱币如图所示,直径约为 40 mm,穿口边长约为 10.5 mm,这枚钱币的面积是多少平方毫米?


答案:
3. $3.14×(40÷2)^{2}-10.5^{2}=1145.75$($mm^{2}$)
查看更多完整答案,请扫码查看


