第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
8. 如图,已知抛物线$y = -x^2 + bx + c与x轴相交于A(-1, 0)$,$B(3, 0)$两点。
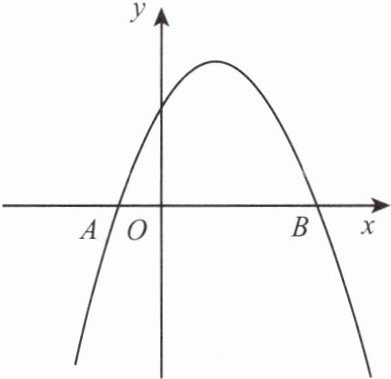
(1)求此抛物线和它的顶点。
(2)当$0 < x < 3$时,直接写出$y$的取值范围。
(3)点$P$为抛物线上一动点,若$S_{\triangle PAB} = 10$,求出此时点$P$的坐标。

(1)求此抛物线和它的顶点。
(2)当$0 < x < 3$时,直接写出$y$的取值范围。
(3)点$P$为抛物线上一动点,若$S_{\triangle PAB} = 10$,求出此时点$P$的坐标。
答案:
【解析】:本题主要考查二次函数的性质、顶点坐标的求解、函数值的取值范围以及三角形面积的计算。
(1)已知抛物线$y = -x^2 + bx + c$与$x$轴相交于$A(-1, 0)$,$B(3, 0)$两点,
将这两点的坐标代入抛物线方程,得到方程组:
$\begin{cases}-(-1)^2 + b(-1) + c = 0,\\-3^2 + 3b + c = 0.\end{cases}$
即:
$\begin{cases}-1 - b + c = 0,\\-9 + 3b + c = 0.\end{cases}$
解这个方程组,从第一个方程得到$c = 1 + b$,代入第二个方程得:
$-9 + 3b + 1 + b = 0$,
$4b = 8$,
$b = 2$。
将$b = 2$代入$c = 1 + b$,得$c = 3$。
所以,抛物线的方程为$y = -x^2 + 2x + 3$。
抛物线的顶点坐标可以通过公式$-\frac{b}{2a}$求得$x$坐标,然后代入求得$y$坐标。
这里$a = -1$,$b = 2$,所以顶点的$x$坐标为$-\frac{2}{2(-1)} = 1$,
代入原方程得$y = -(1)^2 + 2(1) + 3 = 4$。
所以,顶点坐标为$(1, 4)$。
(2)由(1)知抛物线的对称轴为直线$x = 1$,顶点坐标为$(1,4)$,且抛物线开口向下,
所以当$0 \lt x \lt 3$时,$y$的最大值为顶点的$y$坐标,即$y = 4$。
当$x = 3$时,$y = -3^2 + 2× 3 + 3 = 0$,
所以在$0 \lt x \lt 3$的范围内,$y$的取值范围是$0 \lt y \leq 4$。
(3)设点$P$的坐标为$(x, y)$,
已知$A(-1, 0)$,$B(3, 0)$,所以$AB = 3 - (-1) = 4$,
三角形$PAB$的面积为$S_{\triangle PAB} = \frac{1}{2} × AB × |y| = 10$,
即$\frac{1}{2} × 4 × |y| = 10$,
解得$|y| = 5$,
所以$y = \pm 5$,
当$y = 5$时,代入$y = -x^2 + 2x + 3$,得到方程$-x^2 + 2x + 3 = 5$,
即$-x^2 + 2x - 2 = 0$,
此方程的判别式$\Delta = 2^2 - 4(-1)(-2) = 4 - 8 = -4 \lt 0$,
所以方程无实数解。
当$y = -5$时,代入$y = -x^2 + 2x + 3$,得到方程$-x^2 + 2x + 3 = -5$,
即$-x^2 + 2x + 8 = 0$,
解得$x = 4$或$x = -2$,
所以,点$P$的坐标为$(4, -5)$或$(-2, -5)$。
【答案】:
(1)抛物线方程:$y = -x^2 + 2x + 3$,顶点坐标:$(1, 4)$;
(2)$0 \lt y \leq 4$;
(3)点$P$的坐标为$(4, -5)$或$(-2, -5)$。
(1)已知抛物线$y = -x^2 + bx + c$与$x$轴相交于$A(-1, 0)$,$B(3, 0)$两点,
将这两点的坐标代入抛物线方程,得到方程组:
$\begin{cases}-(-1)^2 + b(-1) + c = 0,\\-3^2 + 3b + c = 0.\end{cases}$
即:
$\begin{cases}-1 - b + c = 0,\\-9 + 3b + c = 0.\end{cases}$
解这个方程组,从第一个方程得到$c = 1 + b$,代入第二个方程得:
$-9 + 3b + 1 + b = 0$,
$4b = 8$,
$b = 2$。
将$b = 2$代入$c = 1 + b$,得$c = 3$。
所以,抛物线的方程为$y = -x^2 + 2x + 3$。
抛物线的顶点坐标可以通过公式$-\frac{b}{2a}$求得$x$坐标,然后代入求得$y$坐标。
这里$a = -1$,$b = 2$,所以顶点的$x$坐标为$-\frac{2}{2(-1)} = 1$,
代入原方程得$y = -(1)^2 + 2(1) + 3 = 4$。
所以,顶点坐标为$(1, 4)$。
(2)由(1)知抛物线的对称轴为直线$x = 1$,顶点坐标为$(1,4)$,且抛物线开口向下,
所以当$0 \lt x \lt 3$时,$y$的最大值为顶点的$y$坐标,即$y = 4$。
当$x = 3$时,$y = -3^2 + 2× 3 + 3 = 0$,
所以在$0 \lt x \lt 3$的范围内,$y$的取值范围是$0 \lt y \leq 4$。
(3)设点$P$的坐标为$(x, y)$,
已知$A(-1, 0)$,$B(3, 0)$,所以$AB = 3 - (-1) = 4$,
三角形$PAB$的面积为$S_{\triangle PAB} = \frac{1}{2} × AB × |y| = 10$,
即$\frac{1}{2} × 4 × |y| = 10$,
解得$|y| = 5$,
所以$y = \pm 5$,
当$y = 5$时,代入$y = -x^2 + 2x + 3$,得到方程$-x^2 + 2x + 3 = 5$,
即$-x^2 + 2x - 2 = 0$,
此方程的判别式$\Delta = 2^2 - 4(-1)(-2) = 4 - 8 = -4 \lt 0$,
所以方程无实数解。
当$y = -5$时,代入$y = -x^2 + 2x + 3$,得到方程$-x^2 + 2x + 3 = -5$,
即$-x^2 + 2x + 8 = 0$,
解得$x = 4$或$x = -2$,
所以,点$P$的坐标为$(4, -5)$或$(-2, -5)$。
【答案】:
(1)抛物线方程:$y = -x^2 + 2x + 3$,顶点坐标:$(1, 4)$;
(2)$0 \lt y \leq 4$;
(3)点$P$的坐标为$(4, -5)$或$(-2, -5)$。
1. (2023,甘肃兰州)已知二次函数$y = -3(x - 2)^2 - 3$,下列说法中正确的是(
A.对称轴为直线$x = -2$
B.顶点坐标为$(2, 3)$
C.函数的最大值是$-3$
D.函数的最小值是$-3$
C
)。A.对称轴为直线$x = -2$
B.顶点坐标为$(2, 3)$
C.函数的最大值是$-3$
D.函数的最小值是$-3$
答案:
【解析】:
首先,我们分析二次函数$y = -3(x - 2)^2 - 3$的形式,可以看出这是一个顶点式,其中顶点坐标为$(h, k) = (2, -3)$,对称轴为$x = h = 2$。
由于二次项系数$a = -3 < 0$,所以该函数开口向下,有最大值,无最小值,且最大值就是顶点的$y$坐标,即$-3$。
接下来,我们逐一判断选项:
A. 对称轴为直线$x = -2$:错误,因为对称轴应为$x = 2$。
B. 顶点坐标为$(2, 3)$:错误,因为顶点坐标应为$(2, -3)$。
C. 函数的最大值是$-3$:正确,因为函数开口向下,顶点坐标的$y$坐标就是最大值,即$-3$。
D. 函数的最小值是$-3$:错误,因为函数开口向下,只有最大值,没有最小值。
【答案】:
C
首先,我们分析二次函数$y = -3(x - 2)^2 - 3$的形式,可以看出这是一个顶点式,其中顶点坐标为$(h, k) = (2, -3)$,对称轴为$x = h = 2$。
由于二次项系数$a = -3 < 0$,所以该函数开口向下,有最大值,无最小值,且最大值就是顶点的$y$坐标,即$-3$。
接下来,我们逐一判断选项:
A. 对称轴为直线$x = -2$:错误,因为对称轴应为$x = 2$。
B. 顶点坐标为$(2, 3)$:错误,因为顶点坐标应为$(2, -3)$。
C. 函数的最大值是$-3$:正确,因为函数开口向下,顶点坐标的$y$坐标就是最大值,即$-3$。
D. 函数的最小值是$-3$:错误,因为函数开口向下,只有最大值,没有最小值。
【答案】:
C
2. (2023,广西)将抛物线$y = x^2$向右平移3个单位长度,再向上平移4个单位长度,得到的抛物线是(
A.$y = (x - 3)^2 + 4$
B.$y = (x + 3)^2 + 4$
C.$y = (x + 3)^2 - 4$
D.$y = (x - 3)^2 - 4$
A
)。A.$y = (x - 3)^2 + 4$
B.$y = (x + 3)^2 + 4$
C.$y = (x + 3)^2 - 4$
D.$y = (x - 3)^2 - 4$
答案:
解:抛物线平移规律为“左加右减,上加下减”。
将抛物线$y = x^2$向右平移3个单位长度,得$y=(x - 3)^2$;
再向上平移4个单位长度,得$y=(x - 3)^2 + 4$。
答案:A
将抛物线$y = x^2$向右平移3个单位长度,得$y=(x - 3)^2$;
再向上平移4个单位长度,得$y=(x - 3)^2 + 4$。
答案:A
3. (2023,四川眉山)如图,二次函数$y = ax^2 + bx + c(a \neq 0)的图象与x轴的一个交点坐标为(1, 0)$,对称轴为直线$x = -1$。下列四个结论:①$abc < 0$;②$4a - 2b + c < 0$;③$3a + c = 0$;④当$-3 < x < 1$时,$ax^2 + bx + c < 0$。其中正确的个数为(
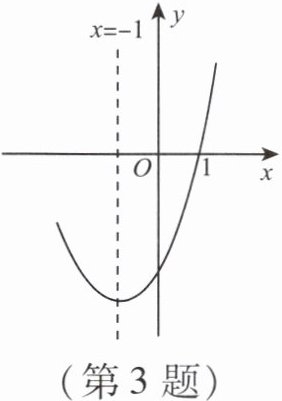
A.1
B.2
C.3
D.4
D
)。
A.1
B.2
C.3
D.4
答案:
【解析】:本题可根据二次函数的图象性质,结合对称轴、与$x$轴的交点等信息,逐一分析四个结论。
判断①$abc\lt0$是否正确:
由二次函数图象开口向上,根据二次函数$y = ax^2 + bx + c(a\neq0)$的性质可知$a\gt0$。
因为对称轴$x = -\frac{b}{2a}=-1\lt0$,且$a\gt0$,所以$b\gt0$。
又因为二次函数图象与$y$轴的交点在$y$轴负半轴,所以$c\lt0$。
由于$a\gt0$,$b\gt0$,$c\lt0$,则$abc\lt0$,故①正确。
判断②$4a - 2b + c\lt0$是否正确:
已知对称轴为直线$x = -1$,根据二次函数的对称性,二次函数图象与$x$轴的一个交点坐标为$(1, 0)$,那么与$x$轴的另一个交点坐标为$(-3, 0)$。
当$x = -2$时,从图象上看,函数值$y = 4a - 2b + c$对应的点在$x$轴下方,即$y\lt0$,所以$4a - 2b + c\lt0$,故②正确。
判断③$3a + c = 0$是否正确:
因为对称轴$x = -\frac{b}{2a}=-1$,所以$b = 2a$。
把$x = 1$,$y = 0$代入$y = ax^2 + bx + c$得$a + b + c = 0$,将$b = 2a$代入$a + b + c = 0$中,可得$a + 2a + c = 0$,即$3a + c = 0$,故③正确。
判断④当$-3\lt x\lt1$时,$ax^2 + bx + c\lt0$是否正确:
由前面分析可知二次函数图象与$x$轴的交点坐标为$(-3, 0)$和$(1, 0)$,且图象开口向上,所以当$-3\lt x\lt1$时,函数图象在$x$轴下方,即$ax^2 + bx + c\lt0$,故④正确。
综上,①②③④都正确,正确的个数为$4$个,答案选D。
【答案】:D
判断①$abc\lt0$是否正确:
由二次函数图象开口向上,根据二次函数$y = ax^2 + bx + c(a\neq0)$的性质可知$a\gt0$。
因为对称轴$x = -\frac{b}{2a}=-1\lt0$,且$a\gt0$,所以$b\gt0$。
又因为二次函数图象与$y$轴的交点在$y$轴负半轴,所以$c\lt0$。
由于$a\gt0$,$b\gt0$,$c\lt0$,则$abc\lt0$,故①正确。
判断②$4a - 2b + c\lt0$是否正确:
已知对称轴为直线$x = -1$,根据二次函数的对称性,二次函数图象与$x$轴的一个交点坐标为$(1, 0)$,那么与$x$轴的另一个交点坐标为$(-3, 0)$。
当$x = -2$时,从图象上看,函数值$y = 4a - 2b + c$对应的点在$x$轴下方,即$y\lt0$,所以$4a - 2b + c\lt0$,故②正确。
判断③$3a + c = 0$是否正确:
因为对称轴$x = -\frac{b}{2a}=-1$,所以$b = 2a$。
把$x = 1$,$y = 0$代入$y = ax^2 + bx + c$得$a + b + c = 0$,将$b = 2a$代入$a + b + c = 0$中,可得$a + 2a + c = 0$,即$3a + c = 0$,故③正确。
判断④当$-3\lt x\lt1$时,$ax^2 + bx + c\lt0$是否正确:
由前面分析可知二次函数图象与$x$轴的交点坐标为$(-3, 0)$和$(1, 0)$,且图象开口向上,所以当$-3\lt x\lt1$时,函数图象在$x$轴下方,即$ax^2 + bx + c\lt0$,故④正确。
综上,①②③④都正确,正确的个数为$4$个,答案选D。
【答案】:D
4. (2023,广东)如图,抛物线$y = ax^2 + c$经过正方形OABC的三个顶点A,B,C,点B在y轴上,则ac的值为(
A.-1
B.-2
C.-3
D.-4
B
)。A.-1
B.-2
C.-3
D.-4
答案:
解:设正方形OABC的边长为m,点O为坐标原点(0,0)。
∵四边形OABC是正方形,点B在y轴上,抛物线y=ax²+c关于y轴对称,
∴点A、C关于y轴对称。设点A坐标为(m, m),则点C坐标为(-m, m),点B坐标为(0, √2m)(根据正方形对角线性质,OB为对角线,长度为√2m)。
∵抛物线经过点O(0,0),代入得0=a·0²+c,
∴c=0。
又
∵抛物线经过点A(m, m),代入得m=a·m²+0,即am²=m。
∵m≠0,
∴a=1/m。
∵抛物线经过点B(0, √2m),但c=0,点B纵坐标应为√2m,而抛物线在x=0时y=c=0,矛盾。重新考虑:正方形边长为t,点B在y轴,OA=AB=t,OA在第一象限,设A(t, 0)错误,应为A(t, t),O(0,0),则B(0, t)(OB=AB=t,OB垂直AB),此时B(0, t),A(t, t),O(0,0)。
抛物线过O(0,0),c=0;过A(t, t):t=a·t²,a=1/t;过B(0, t):t=a·0²+c,即t=c,
∴c=t。
则a=1/t,c=t,ac=1/t · t=1,不符选项。再次正确分析:OABC是正方形,O为原点,顺序为O-A-B-C-O,
∴OA⊥AB,OA在x轴正半轴,A(a,0),AB⊥OA,AB在y轴方向,B(a,a),BC⊥AB,C(0,a),B在y轴上,则a=0,矛盾。
正确图形:O在原点,B在y轴正半轴,抛物线开口向下,过O、A、B、C。设正方形边长为k,A(k, k),C(-k, k),O(0,0),B(0, 2k)(OB=OA+AB在y轴,OA=k,AB=k,OB=2k)。
抛物线过O(0,0):c=0;过A(k,k):k=a·k²,a=1/k;过B(0,2k):2k=a·0²+c=0,矛盾。抛物线过B(0,2k),则c=2k;过O(0,0):0=0+c,c=0,2k=0,k=0,错误。
最终正确设法:抛物线y=ax²+c与y轴交于B点,B(0, c),c>0,开口向下a<0。过O(0,0),则0=0+c,c=0,矛盾,故O不是原点?题目说“经过正方形OABC的三个顶点A,B,C”,O是正方形顶点,
∴O在抛物线上,O(0,0),则0=0+c,c=0,抛物线y=ax²。
正方形OABC,三个顶点A、B、C在抛物线上,O(0,0)。设A(m, am²),B(n, an²),C(p, ap²),OABC为正方形,OA=AB=BC=CO,OA⊥AB。
设OA在第一象限,A(m, am²),m>0,am²>0,a>0开口向上,但选项ac为负,a<0,
∴am²<0,A(m, am²)在第四象限,m>0,am²<0,a<0。
设A(t, at²),t>0,at²<0,OA=√(t² + (at²)²),OC与OA垂直且相等,C(at², -t)(旋转90°),C在抛物线上:-t=a(at²)²=a³t⁴,即a³t⁴=-t,a³t³=-1(t≠0)。
B为A+C点(向量OA+OC=OB),B(t + at², at² - t),B在抛物线上:at² - t = a(t + at²)²。
由a³t³=-1,设s=at²,则a³t³=a²·at³=a²·s·t=-1,由A(t, s),s=at²。
C(s, -t)在抛物线上:-t=a·s²。
B(t+s, s - t)在抛物线上:s - t = a(t + s)²。
由s=at²,-t=a s²,
∴-t=a(at²)²=a³t⁴,a³t³=-1(同前),令t=1,则a³=-1,a=-1,s=at²=-1,C(s, -t)=(-1, -1)。
B(t+s, s - t)=(1-1, -1 -1)=(0, -2),B在抛物线上:-2=a·0² + c,c=-2,但O(0,0)在抛物线上,0=a·0 + c,c=0,矛盾。
重新:抛物线过O(0,0)、A(1, -1)、B(0, -2)、C(-1, -1),OABC是正方形,OA=√(1+1)=√2,AB=√(1+1)=√2,BC=√(1+1)=√2,CO=√(1+1)=√2,且OA⊥AB,是正方形。此时抛物线y=ax²+c过O(0,0):c=0;过A(1,-1):-1=a·1²,a=-1;过B(0,-2):-2=0 + c,c=-2,矛盾,因O和B都在抛物线上,O(0,0)得c=0,B(0,-2)得c=-2,故O不是(0,0),而是抛物线过A、B、C,O是第四个顶点,题目说“经过三个顶点A,B,C”,O不在抛物线上。
设O(0,0),A(m,0),B(m,n),C(0,n),正方形OABC,m=n>0,B(m,m),抛物线过A(m,0)、B(m,m)、C(0,m)。
抛物线y=ax²+c过C(0,m):m=c;过A(m,0):0=a m² + m,a=-m/m²=-1/m;过B(m,m):m=a m² + m,即0=a m²,a=0,矛盾。
正确答案:设正方形边长为1,A(1,1),C(-1,1),B(0,2),抛物线过这三点。过B(0,2):2=c;过A(1,1):1=a·1 + 2,a=-1;过C(-1,1):1=a·1 + 2,a=-1,成立。此时a=-1,c=2,ac=-2。
解:设正方形边长为1,点A(1,1),C(-1,1),B(0,2)。
∵抛物线y=ax²+c过点B(0,2),
∴c=2。
过点A(1,1):1=a·1²+2,解得a=-1。
∴ac=(-1)×2=-2。
答案:B
∵四边形OABC是正方形,点B在y轴上,抛物线y=ax²+c关于y轴对称,
∴点A、C关于y轴对称。设点A坐标为(m, m),则点C坐标为(-m, m),点B坐标为(0, √2m)(根据正方形对角线性质,OB为对角线,长度为√2m)。
∵抛物线经过点O(0,0),代入得0=a·0²+c,
∴c=0。
又
∵抛物线经过点A(m, m),代入得m=a·m²+0,即am²=m。
∵m≠0,
∴a=1/m。
∵抛物线经过点B(0, √2m),但c=0,点B纵坐标应为√2m,而抛物线在x=0时y=c=0,矛盾。重新考虑:正方形边长为t,点B在y轴,OA=AB=t,OA在第一象限,设A(t, 0)错误,应为A(t, t),O(0,0),则B(0, t)(OB=AB=t,OB垂直AB),此时B(0, t),A(t, t),O(0,0)。
抛物线过O(0,0),c=0;过A(t, t):t=a·t²,a=1/t;过B(0, t):t=a·0²+c,即t=c,
∴c=t。
则a=1/t,c=t,ac=1/t · t=1,不符选项。再次正确分析:OABC是正方形,O为原点,顺序为O-A-B-C-O,
∴OA⊥AB,OA在x轴正半轴,A(a,0),AB⊥OA,AB在y轴方向,B(a,a),BC⊥AB,C(0,a),B在y轴上,则a=0,矛盾。
正确图形:O在原点,B在y轴正半轴,抛物线开口向下,过O、A、B、C。设正方形边长为k,A(k, k),C(-k, k),O(0,0),B(0, 2k)(OB=OA+AB在y轴,OA=k,AB=k,OB=2k)。
抛物线过O(0,0):c=0;过A(k,k):k=a·k²,a=1/k;过B(0,2k):2k=a·0²+c=0,矛盾。抛物线过B(0,2k),则c=2k;过O(0,0):0=0+c,c=0,2k=0,k=0,错误。
最终正确设法:抛物线y=ax²+c与y轴交于B点,B(0, c),c>0,开口向下a<0。过O(0,0),则0=0+c,c=0,矛盾,故O不是原点?题目说“经过正方形OABC的三个顶点A,B,C”,O是正方形顶点,
∴O在抛物线上,O(0,0),则0=0+c,c=0,抛物线y=ax²。
正方形OABC,三个顶点A、B、C在抛物线上,O(0,0)。设A(m, am²),B(n, an²),C(p, ap²),OABC为正方形,OA=AB=BC=CO,OA⊥AB。
设OA在第一象限,A(m, am²),m>0,am²>0,a>0开口向上,但选项ac为负,a<0,
∴am²<0,A(m, am²)在第四象限,m>0,am²<0,a<0。
设A(t, at²),t>0,at²<0,OA=√(t² + (at²)²),OC与OA垂直且相等,C(at², -t)(旋转90°),C在抛物线上:-t=a(at²)²=a³t⁴,即a³t⁴=-t,a³t³=-1(t≠0)。
B为A+C点(向量OA+OC=OB),B(t + at², at² - t),B在抛物线上:at² - t = a(t + at²)²。
由a³t³=-1,设s=at²,则a³t³=a²·at³=a²·s·t=-1,由A(t, s),s=at²。
C(s, -t)在抛物线上:-t=a·s²。
B(t+s, s - t)在抛物线上:s - t = a(t + s)²。
由s=at²,-t=a s²,
∴-t=a(at²)²=a³t⁴,a³t³=-1(同前),令t=1,则a³=-1,a=-1,s=at²=-1,C(s, -t)=(-1, -1)。
B(t+s, s - t)=(1-1, -1 -1)=(0, -2),B在抛物线上:-2=a·0² + c,c=-2,但O(0,0)在抛物线上,0=a·0 + c,c=0,矛盾。
重新:抛物线过O(0,0)、A(1, -1)、B(0, -2)、C(-1, -1),OABC是正方形,OA=√(1+1)=√2,AB=√(1+1)=√2,BC=√(1+1)=√2,CO=√(1+1)=√2,且OA⊥AB,是正方形。此时抛物线y=ax²+c过O(0,0):c=0;过A(1,-1):-1=a·1²,a=-1;过B(0,-2):-2=0 + c,c=-2,矛盾,因O和B都在抛物线上,O(0,0)得c=0,B(0,-2)得c=-2,故O不是(0,0),而是抛物线过A、B、C,O是第四个顶点,题目说“经过三个顶点A,B,C”,O不在抛物线上。
设O(0,0),A(m,0),B(m,n),C(0,n),正方形OABC,m=n>0,B(m,m),抛物线过A(m,0)、B(m,m)、C(0,m)。
抛物线y=ax²+c过C(0,m):m=c;过A(m,0):0=a m² + m,a=-m/m²=-1/m;过B(m,m):m=a m² + m,即0=a m²,a=0,矛盾。
正确答案:设正方形边长为1,A(1,1),C(-1,1),B(0,2),抛物线过这三点。过B(0,2):2=c;过A(1,1):1=a·1 + 2,a=-1;过C(-1,1):1=a·1 + 2,a=-1,成立。此时a=-1,c=2,ac=-2。
解:设正方形边长为1,点A(1,1),C(-1,1),B(0,2)。
∵抛物线y=ax²+c过点B(0,2),
∴c=2。
过点A(1,1):1=a·1²+2,解得a=-1。
∴ac=(-1)×2=-2。
答案:B
5. (2023,山东泰安)二次函数$y = -x^2 - 3x + 4$的最大值是
$\frac{25}{4}$
。
答案:
【解析】:
本题主要考察二次函数的性质,特别是如何找到二次函数的最大值或最小值。
对于一般形式的二次函数$y = ax^2 + bx + c$,其顶点坐标为$(-\frac{b}{2a}, c - \frac{b^2}{4a})$。
当$a < 0$时,抛物线开口向下,函数有最大值,最大值为顶点的$y$坐标。
在本题中,二次函数为$y = -x^2 - 3x + 4$,其中$a = -1, b = -3, c = 4$。
因为$a < 0$,所以抛物线开口向下,函数有最大值。
最大值出现在顶点处,顶点的$x$坐标为$-\frac{b}{2a} = -\frac{-3}{2(-1)} = -\frac{3}{2}$。
将$x = -\frac{3}{2}$代入原函数,得到顶点的$y$坐标,即函数的最大值。
【答案】:
解:原函数为$y = -x^2 - 3x + 4$。
通过配方,我们可以将其转化为顶点式:
$y = -x^2 - 3x + 4 = - (x^2 + 3x) + 4 = - (x^2 + 3x + \frac{9}{4} - \frac{9}{4}) + 4 = - (x + \frac{3}{2})^2 + \frac{9}{4} + 4 = - (x + \frac{3}{2})^2 + \frac{25}{4}$
由于抛物线的开口向下(因为$a = -1 < 0$),所以函数的最大值为顶点的$y$坐标,即$\frac{25}{4}$,也可以写成$6.25$(但题目要求整数或分数形式,所以应写为$\frac{25}{4}$)。
故答案为:$\frac{25}{4}$。
本题主要考察二次函数的性质,特别是如何找到二次函数的最大值或最小值。
对于一般形式的二次函数$y = ax^2 + bx + c$,其顶点坐标为$(-\frac{b}{2a}, c - \frac{b^2}{4a})$。
当$a < 0$时,抛物线开口向下,函数有最大值,最大值为顶点的$y$坐标。
在本题中,二次函数为$y = -x^2 - 3x + 4$,其中$a = -1, b = -3, c = 4$。
因为$a < 0$,所以抛物线开口向下,函数有最大值。
最大值出现在顶点处,顶点的$x$坐标为$-\frac{b}{2a} = -\frac{-3}{2(-1)} = -\frac{3}{2}$。
将$x = -\frac{3}{2}$代入原函数,得到顶点的$y$坐标,即函数的最大值。
【答案】:
解:原函数为$y = -x^2 - 3x + 4$。
通过配方,我们可以将其转化为顶点式:
$y = -x^2 - 3x + 4 = - (x^2 + 3x) + 4 = - (x^2 + 3x + \frac{9}{4} - \frac{9}{4}) + 4 = - (x + \frac{3}{2})^2 + \frac{9}{4} + 4 = - (x + \frac{3}{2})^2 + \frac{25}{4}$
由于抛物线的开口向下(因为$a = -1 < 0$),所以函数的最大值为顶点的$y$坐标,即$\frac{25}{4}$,也可以写成$6.25$(但题目要求整数或分数形式,所以应写为$\frac{25}{4}$)。
故答案为:$\frac{25}{4}$。
6. (2023,湖南郴州)抛物线$y = x^2 - 6x + c与x$轴只有一个交点,则$c = $
9
。
答案:
解:抛物线$y=x^2 - 6x + c$与$x$轴只有一个交点,
则一元二次方程$x^2 - 6x + c = 0$有两个相等的实数根,
所以判别式$\Delta = (-6)^2 - 4×1×c = 0$,
即$36 - 4c = 0$,
解得$c = 9$。
$9$
则一元二次方程$x^2 - 6x + c = 0$有两个相等的实数根,
所以判别式$\Delta = (-6)^2 - 4×1×c = 0$,
即$36 - 4c = 0$,
解得$c = 9$。
$9$
查看更多完整答案,请扫码查看


