《2025年云南省标准教辅优佳学案九年级数学上册人教版》

9.(2023,四川南充)已知关于$x的一元二次方程x^{2}-(2m-1)x-3m^{2}+m= 0$.
(1)求证：无论$m$为何值,方程总有实数根.
(2)若$x_1,x_2$是方程的两个实数根,且$\frac{x_2}{x_1}+\frac{x_1}{x_2}= -\frac{5}{2}$,求$m$的值.

答案：
(1)证明：
$\Delta = [-(2m-1)]^2 - 4 × 1 × (-3m^2 + m)$
$= 4m^2 - 4m + 1 + 12m^2 - 4m$
$= 16m^2 - 8m + 1$
$=(4m - 1)^2 \geq 0$
∴无论$m$为何值，方程总有实数根.
(2)解：
由韦达定理得$x_1 + x_2 = 2m - 1$，$x_1x_2 = -3m^2 + m$.
$\frac{x_2}{x_1} + \frac{x_1}{x_2} = \frac{x_1^2 + x_2^2}{x_1x_2} = \frac{(x_1 + x_2)^2 - 2x_1x_2}{x_1x_2} = -\frac{5}{2}$
代入得$\frac{(2m - 1)^2 - 2(-3m^2 + m)}{-3m^2 + m} = -\frac{5}{2}$
化简分子：$4m^2 - 4m + 1 + 6m^2 - 2m = 10m^2 - 6m + 1$
方程化为$\frac{10m^2 - 6m + 1}{-3m^2 + m} = -\frac{5}{2}$
两边乘$2(-3m^2 + m)$：$2(10m^2 - 6m + 1) = 5(3m^2 - m)$
$20m^2 - 12m + 2 = 15m^2 - 5m$
$5m^2 - 7m + 2 = 0$
$(5m - 2)(m - 1) = 0$
解得$m = 1$或$m = \frac{2}{5}$
检验：当$m = 1$时，$x_1x_2 = -3 + 1 = -2 \neq 0$；当$m = \frac{2}{5}$时，$x_1x_2 = -3(\frac{4}{25}) + \frac{2}{5} = -\frac{12}{25} + \frac{10}{25} = -\frac{2}{25} \neq 0$
∴$m = 1$或$m = \frac{2}{5}$

10.(2023,湖南郴州)随着旅游旺季的到来,某景区游客人数逐月增加,2月份游客人数为1.6万人,4月份游客人数为2.5万人.
(1)求这两个月中该景区游客人数的月平均增长率.
(2)预计5月份该景区游客人数会继续增长,但增长率不会超过前两个月的月平均增长率. 已知该景区5月1日至5月21日已接待游客2.125万人,则5月份后10天日均接待游客人数最多是多少万人？

答案： 【解析】：
(1) 主要考察一元二次方程的应用（增长率问题）。
设该景区游客人数的月平均增长率为$x$，则可以根据公式：$后续人数 = 初始人数 × (1 + 增长率)^{月数}$，列出方程$1.6(1 + x)^{2} = 2.5$，通过求解这个方程，可以得到$x$的值，即月平均增长率。
(2) 主要考察不等式的应用。
首先，需要计算出5月份前21天的日均增长率，然后根据题目条件“增长率不会超过前两个月的月平均增长率”列出不等式，求解出5月份后10天的日均接待游客人数最多是多少。
【答案】：
(1) 设该景区游客人数的月平均增长率为$x$，
依题意得：$1.6(1 + x)^{2} = 2.5$，
整理得：$(1 + x)^{2} = \frac{25}{16}$，
开方得：$1 + x = \pm\frac{5}{4}$，
解得：$x_{1} = \frac{5}{4} - 1 = 0.25 = 25\%$，$x_{2} = -\frac{5}{4} - 1 = -2.25$（不合题意，舍去）。
答：这两个月中该景区游客人数的月平均增长率为$25\%$。
(2) 设5月份后10天日均接待游客$y$万人，
则$2.125 + 10y \leq 2.5 × (1 + 25\%)$，
整理得：$2.125 + 10y \leq 3.125$，
移项得：$10y \leq 1$，
解得：$y \leq 0.1$。
答：5月份后10天日均接待游客人数最多是0.1万人。

11.(2023,山东东营)如图,老李想用长为70m的栅栏,再借助房屋的外墙(外墙足够长)围成一个矩形羊圈$ABCD$,并在边$BC$上留一扇2m宽的门(建在$EF$处,另用其他材料).
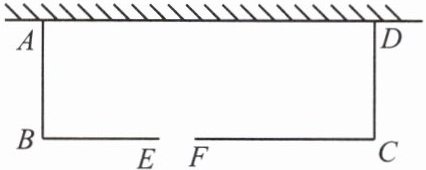
(1)当羊圈的长和宽分别为多少米时,能围成一个面积为$640m^{2}$的羊圈？
(2)羊圈的面积能达到$650m^{2}$吗？如果能,请你给出设计方案；如果不能,请说明理由.

答案： 【解析】：本题主要考查一元二次方程的实际应用。
(1) 设$AB$的长度为$x$米，由于总长是$70m$，并且有一扇$2m$宽的门，所以$BC$的长度为$(70-2x+2)$米，即$(72-2x)$米。
根据面积为$640m^2$，我们可以列出方程：
$x(72 - 2x) = 640$，
展开并整理得：
$72x - 2x^2 = 640$，
$2x^2 - 72x + 640 = 0$，
$x^2 - 36x + 320 = 0$，
通过因式分解，我们得到：
$(x - 16)(x - 20) = 0$，
解得：$x_1 = 16, x_2 = 20$。
当$x = 16$时，$72-2x = 72-2×16 = 40$；
当$x = 20$时，$72-2x = 72-2×20 = 32$。
所以当羊圈的长为$40m$，宽为$16m$，或长为$32m$，宽为$20m$时，能围成一个面积为$640m^2$的羊圈。
(2) 设$AB$的长度为$y$米，则$BC$的长度为$(72-2y)$米。
根据面积为$650m^2$，我们可以列出方程：
$y(72 - 2y) = 650$，
展开并整理得：
$72y - 2y^2 = 650$，
$2y^2 - 72y + 650 = 0$，
$y^2 - 36y + 325 = 0$。
接下来，我们计算判别式来判断这个方程是否有实数解：
$\Delta = b^2 - 4ac = (-36)^2 - 4 × 1 × 325 = 1296 - 1300 = -4$，
由于$\Delta ＜ 0$，所以这个方程没有实数解。
因此，羊圈的面积不能达到$650m^2$。
【答案】：
(1)当羊圈的长为$40m$，宽为$16m$，或长为$32m$，宽为$20m$时，能围成一个面积为$640m^2$的羊圈。
(2)羊圈的面积不能达到$650m^2$。