《2025年云南省标准教辅优佳学案九年级数学上册人教版》

【例题1】下列函数中,哪些是关于$x$的二次函数？
①$y = 1 - 3x^{2}$.
②$y = 3x^{2} + 2x$.
③$y = \frac{1}{x^{2}}$.
④$y = x(x - 5) + 2$.
⑤$y = x + \frac{1}{x}$.
⑥$x^{2} - y + 2 = 0$.
⑦$y = (x - 1)^{2} - (x + 1)(x - 2)$.

答案： 思路导引 判断一个函数是否为二次函数,要先化简整理,然后再根据定义进行判断.在判断是否是二次函数的问题中,应紧紧抓住三个要点：函数含两个变量,这两个变量符合函数的对应关系；函数解析式右边是整式；自变量次数最高为2.
解：①②④⑥是关于$x$的二次函数.

【例题2】已知函数$y = (m - 1)x^{m^{2} + 1} + 5x - 3$是二次函数,求$m$的值.

答案： 思路导引 解答这类题,既需要考虑函数解析式的最高次项的次数为2,也需要考虑二次项系数不能为0.
解：$\because y = (m - 1)x^{m^{2} + 1} + 5x - 3$是二次函数,$\therefore m^{2} + 1 = 2且m - 1 \neq 0.\therefore m = - 1$.

【例题3】某物体从上午7时至下午4时的温度$M$(单位：$^{\circ}C$)是时间$t$(单位：$h$)的函数：$M = - 2t^{2} - 5t + 100$(其中$t = 0$表示中午12时,$t = 1$表示下午1时),则上午10时此物体的温度为102$^{\circ}C$.

答案： 思路导引 理解规定的含义,$t = 0$表示中午12时,$t = 1$表示下午1时,那么$t = - 1$表示上午11时,$\therefore$上午10时,$t = - 2$.此时$M = - 2( - 2)^{2} - 5 × ( - 2) + 100 = 102$.
$\therefore$上午10时此物体的温度为$102^{\circ}C$.
答案：102.

1. 下列函数中,是二次函数的是(D).
A.$y = \frac{1}{x}$
B.$y = ax^{2} + bx + c$
C.$y = x^{3} - 2x$
D.$y = 2x^{2} - x$

答案： 解：二次函数的一般形式为$y = ax^2 + bx + c$（$a$、$b$、$c$是常数，$a \neq 0$）。
选项A：$y = \frac{1}{x}$是反比例函数，不是二次函数。
选项B：当$a = 0$时，$y = ax^2 + bx + c$不是二次函数，所以该选项不一定是二次函数。
选项C：$y = x^3 - 2x$中$x$的最高次数是3，是三次函数，不是二次函数。
选项D：$y = 2x^2 - x$符合二次函数的一般形式，其中$a = 2 \neq 0$，是二次函数。
答案：D

2. 已知$y = (m + 1)x^{m^{2} + 1} + 2x - 3$是二次函数,则$m$的值为(B).
A.0
B.1
C.-1
D.1或-1

答案： 解：因为$y = (m + 1)x^{m^{2} + 1} + 2x - 3$是二次函数，所以需满足：
1. 自变量$x$的最高次数为$2$，即$m^{2} + 1 = 2$，解得$m = 1$或$m = -1$；
2. 二次项系数不为$0$，即$m + 1 \neq 0$，解得$m \neq -1$。
综上，$m = 1$。
答案：B

3. 已知二次函数$y = - x^{2} + bx + 3$,当$x = 2$时,$y = 3$,则这个二次函数的解析式是______.
$y=-x^{2}+2x + 3$

答案： 解：将$x = 2$，$y = 3$代入$y=-x^{2}+bx + 3$，得$3=-(2)^{2}+2b + 3$，即$3=-4 + 2b + 3$，解得$b = 2$，所以二次函数解析式为$y=-x^{2}+2x + 3$。
$y=-x^{2}+2x + 3$

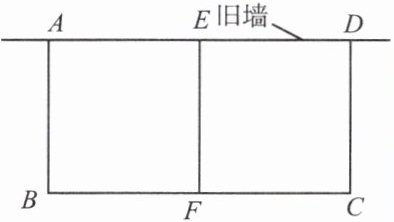
4. 如图是一个矩形花圃的平面图,花圃由一堵旧墙(旧墙的长度不小于30 m)和总长为28 m的篱笆围成,中间用篱笆分隔成两个小矩形. 设大矩形的垂直于旧墙的一边长为$x$ m,花圃的总面积为$y$ $m^{2}$,求$y关于x$的函数解析式(用二次函数的一般式表示).

答案： 【解析】：本题需要根据矩形面积公式列出函数关系式，需要用到矩形面积公式和二次函数一般式。
首先，确定矩形花圃的各个边长。
已知大矩形垂直于旧墙的一边长为$x$米。
由于篱笆总长为$28$米，且中间用篱笆分隔成两个小矩形，
因此，平行于旧墙的一边长为$(28 - 3x)$米（因为两个垂直边各用了$x$米的篱笆，中间分隔用了$x$米的篱笆，所以剩下的篱笆长度为$28 - 3x$米，这就是平行于旧墙的一边的长度）。
确定花圃的总面积。
根据矩形面积公式：$面积 = 长× 宽$，可以得到：
$y = x(28 - 3x)$，
展开得：
$y = 28x - 3x^{2}$。
根据题目条件，旧墙的长度不小于$30$米，但这个条件在求解函数解析式时并不直接用到，它更多地是用于确定$x$的取值范围（即$28 - 3x \leq 30$，解得$x \geq \frac{2}{3} × (28 - 30) =\frac{-2}{3}× -2= \frac{4}{3} × 2 = \frac{8}{3} \approx 2.67$，但由于$x$表示长度，所以$x$必须大于$0$，且由于$28 - 3x$也必须大于$0$，所以$x ＜ \frac{28}{3}$）。
但在这个问题中，只需求出函数解析式，所以不需要进一步确定$x$的具体取值范围。
【答案】：$y$关于$x$的函数解析式为$y = -3x^{2} + 28x$。