第123页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
【例题1】如图①,有一个圆锥形粮堆,其轴截面是边长为6 m的等边三角形ABC,粮堆母线AC的中点P处有一只老鼠正在偷吃粮食. 此时小猫在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所走的最短路线的长是多少?
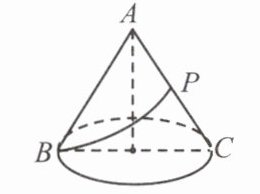

答案:
思路导引 在圆锥上观察最短路线比较困难,可以求出圆锥的侧面展开图的圆心角,画出侧面展开图,根据两点之间线段最短,连接BP,BP的长即小猫所走的最短路线.
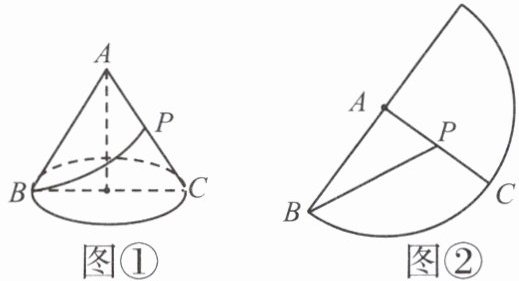
解:设圆锥底面圆的半径为r,母线长为l,展开后扇形的圆心角度数为n°,则底面圆的周长为$2\pi r$,扇形的弧长为$\frac{n\pi l}{180}$,$\therefore 2\pi r = \frac{n\pi l}{180}$.
$\because轴截面\triangle ABC$为等边三角形,$\therefore AB = AC$,即$l = 2r = 6(m)$. $\therefore r = 3(m)$. 将$r = 3$,$l = 6$. 代入$2\pi r = \frac{n\pi l}{180}$,得$2\pi × 3 = \frac{n\pi × 6}{180}$. 解得$n = 180$. 即圆锥的侧面展开图为半圆,如图②,则$\triangle ABP$为直角三角形,BP为最短路线.
在Rt $\triangle ABP$中,$BP = \sqrt{AB^2 + AP^2} = \sqrt{6^2 + 3^2} = 3\sqrt{5}(m)$. 因此小猫所走的最短路线的长是$3\sqrt{5}$ m.
思路导引 在圆锥上观察最短路线比较困难,可以求出圆锥的侧面展开图的圆心角,画出侧面展开图,根据两点之间线段最短,连接BP,BP的长即小猫所走的最短路线.

解:设圆锥底面圆的半径为r,母线长为l,展开后扇形的圆心角度数为n°,则底面圆的周长为$2\pi r$,扇形的弧长为$\frac{n\pi l}{180}$,$\therefore 2\pi r = \frac{n\pi l}{180}$.
$\because轴截面\triangle ABC$为等边三角形,$\therefore AB = AC$,即$l = 2r = 6(m)$. $\therefore r = 3(m)$. 将$r = 3$,$l = 6$. 代入$2\pi r = \frac{n\pi l}{180}$,得$2\pi × 3 = \frac{n\pi × 6}{180}$. 解得$n = 180$. 即圆锥的侧面展开图为半圆,如图②,则$\triangle ABP$为直角三角形,BP为最短路线.
在Rt $\triangle ABP$中,$BP = \sqrt{AB^2 + AP^2} = \sqrt{6^2 + 3^2} = 3\sqrt{5}(m)$. 因此小猫所走的最短路线的长是$3\sqrt{5}$ m.
【例题2】如图,从一块直径为2的圆形铁皮中剪下一个圆心角为90°的扇形.(1)求这个扇形的面积(结果保留$\pi$).(2)在剩下的三块余料中,能否从第③块余料中剪下一个圆作为底面与此扇形围成一个圆锥?
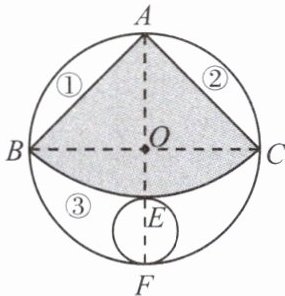

答案:
思路导引 求扇形的面积和对应圆锥底面圆的直径是解题的关键.
解:设扇形的半径为R,小圆的半径为r.
(1)连接BC. 由勾股定理,得$AB = AC = R = \sqrt{2}$,$\therefore S_{扇形} = \frac{90\pi R^2}{360} = \frac{90\pi × (\sqrt{2})^2}{360} = \frac{1}{2}\pi$.
(2)连接AO并延长与BC和$\odot O$相交于点E,F,则$EF = AF - AE = 2 - \sqrt{2}$. $\widehat{BC} = \frac{n\pi R}{180} = \frac{90\pi × \sqrt{2}}{180} = \frac{\sqrt{2}}{2}\pi$. $\because 2\pi r = \frac{\sqrt{2}}{2}\pi$,$\therefore圆锥底面圆的直径为2r = \frac{\sqrt{2}}{2}$. $\because 2 - \sqrt{2} < \frac{\sqrt{2}}{2}$,$\therefore$不能从第③块余料中剪下一个圆作为底面与此扇形围成一个圆锥.
解:设扇形的半径为R,小圆的半径为r.
(1)连接BC. 由勾股定理,得$AB = AC = R = \sqrt{2}$,$\therefore S_{扇形} = \frac{90\pi R^2}{360} = \frac{90\pi × (\sqrt{2})^2}{360} = \frac{1}{2}\pi$.
(2)连接AO并延长与BC和$\odot O$相交于点E,F,则$EF = AF - AE = 2 - \sqrt{2}$. $\widehat{BC} = \frac{n\pi R}{180} = \frac{90\pi × \sqrt{2}}{180} = \frac{\sqrt{2}}{2}\pi$. $\because 2\pi r = \frac{\sqrt{2}}{2}\pi$,$\therefore圆锥底面圆的直径为2r = \frac{\sqrt{2}}{2}$. $\because 2 - \sqrt{2} < \frac{\sqrt{2}}{2}$,$\therefore$不能从第③块余料中剪下一个圆作为底面与此扇形围成一个圆锥.
查看更多完整答案,请扫码查看


