第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
【例题1】已知一抛物线与$x轴相交于点A(-2, 0)$,$B(1, 0)$,且经过点$C(2, 8)$,求该抛物线对应的函数解析式。
答案:
思路导引:该抛物线经过$A$,$B$,$C$三点,可用一般式来求解。经过观察,又知$A$,$B两点是抛物线与x$轴的交点,故又可用交点式来求解。总之,用待定系数法求函数解析式,一定要根据题目特征灵活选用关系式。
解:方法一:设该抛物线对应的函数解析式为$y = ax^2 + bx + c(a \neq 0)$。
由抛物线经过点$A(-2, 0)$,$B(1, 0)$,$C(2, 8)$,得$\begin{cases}4a - 2b + c = 0\\a + b + c = 0\\4a + 2b + c = 8\end{cases} $,解得$\begin{cases}a = 2\\b = 2\\c = -4\end{cases} $。
故该抛物线对应的函数解析式为$y = 2x^2 + 2x - 4$。
方法二:抛物线与$x轴交于点A(-2, 0)$,$B(1, 0)$,设$y = a(x + 2)(x - 1)(a \neq 0)$。
由抛物线经过点$C(2, 8)$,得$8 = a(2 + 2)(2 - 1)$。解得$a = 2$。
所以$y = 2(x + 2)(x - 1)$。
整理,得$y = 2x^2 + 2x - 4$。
故该抛物线对应的函数解析式为$y = 2x^2 + 2x - 4$。
解:方法一:设该抛物线对应的函数解析式为$y = ax^2 + bx + c(a \neq 0)$。
由抛物线经过点$A(-2, 0)$,$B(1, 0)$,$C(2, 8)$,得$\begin{cases}4a - 2b + c = 0\\a + b + c = 0\\4a + 2b + c = 8\end{cases} $,解得$\begin{cases}a = 2\\b = 2\\c = -4\end{cases} $。
故该抛物线对应的函数解析式为$y = 2x^2 + 2x - 4$。
方法二:抛物线与$x轴交于点A(-2, 0)$,$B(1, 0)$,设$y = a(x + 2)(x - 1)(a \neq 0)$。
由抛物线经过点$C(2, 8)$,得$8 = a(2 + 2)(2 - 1)$。解得$a = 2$。
所以$y = 2(x + 2)(x - 1)$。
整理,得$y = 2x^2 + 2x - 4$。
故该抛物线对应的函数解析式为$y = 2x^2 + 2x - 4$。
【例题2】已知二次函数$y = ax^2 + bx + c$的图象如图所示,则下列结论中正确的是(
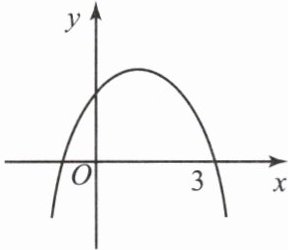
A.$a > 0$
B.$c < 0$
C.$b^2 - 4ac < 0$
D.$a + b + c > 0$
D
)。
A.$a > 0$
B.$c < 0$
C.$b^2 - 4ac < 0$
D.$a + b + c > 0$
答案:
思路导引:解答此类问题,要熟练掌握抛物线的开口方向、位置、对称轴、特殊值等,分析判断时一定要应用数形结合的思想,常用规律有:①$a$的正、负决定抛物线的开口方向:当$a > 0$时,开口向上;当$a < 0$时,开口向下。②$a$,$b$共同决定抛物线对称轴的位置:当$a$,$b$同号时,对称轴在$y$轴左侧;当$a$,$b$异号时,对称轴在$y$轴右侧;当$b = 0$时,对称轴为$y$轴。简记为“左同右异”。③$c决定抛物线与y$轴的交点位置:当$c > 0$时,抛物线与$y$轴交于正半轴;当$c < 0$时,抛物线与$y$轴交于负半轴;当$c = 0$时,抛物线过原点。④$b^2 - 4ac决定抛物线与x$轴的交点个数:当$b^2 - 4ac > 0$时,抛物线与$x$轴有两个交点;当$b^2 - 4ac < 0$时,抛物线与$x$轴没有交点;当$b^2 - 4ac = 0$时,抛物线与$x$轴有一个交点。⑤若抛物线经过点$(1, 0)$,则$a + b + c = 0$;若抛物线经过点$(-1, 0)$,则$a - b + c = 0$。
答案:D。
答案:D。
【例题3】某公司销售一种新型节能产品,现准备从国内销售方案和国外销售方案两种方案中选择一种进行销售。若只在国内销售,销售价格$y$(单位:元/件)与月销量$x$(单位:件)之间的函数解析式为$y = -\frac{1}{100}x + 150$。成本为20元/件,无论销售多少,每月还需支出广告费62500元。设国内销售的月利润为$w_{内}$元(利润= 销售额-成本-广告费)。若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为$a$元/件($a$为常数,$10 \leq a \leq 40$),当月销量为$x$件时,每月还需缴纳$\frac{1}{100}x^2$元的附加费。设国外销售的月利润为$w_{外}$元(利润= 销售额-成本-附加费)。
(1)当$x = 1000$时,$y = $
(2)分别求出$w_{内}$,$w_{外}与x$之间的函数解析式(不必写$x$的取值范围)。
(3)当$x$为何值时,在国内销售的月利润最大?若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求$a$的值。
(4)如果某月要将5000件产品全部销售完,请你通过分析帮公司决策,选择在国内还是在国外销售才能使所获月利润较大?
(1)当$x = 1000$时,$y = $
140
元/件,$w_{内} = $57500
元。(2)分别求出$w_{内}$,$w_{外}与x$之间的函数解析式(不必写$x$的取值范围)。
解:$w_{内}=x(y - 20)-62500$
$=x\left(-\frac{1}{100}x + 150 - 20\right)-62500$
$=-\frac{1}{100}x^{2}+130x - 62500$
$w_{外}=x(150 - a)-\frac{1}{100}x^{2}$
$=-\frac{1}{100}x^{2}+(150 - a)x$
$=x\left(-\frac{1}{100}x + 150 - 20\right)-62500$
$=-\frac{1}{100}x^{2}+130x - 62500$
$w_{外}=x(150 - a)-\frac{1}{100}x^{2}$
$=-\frac{1}{100}x^{2}+(150 - a)x$
(3)当$x$为何值时,在国内销售的月利润最大?若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求$a$的值。
解:对于$w_{内}=-\frac{1}{100}x^{2}+130x - 62500$,$a=-\frac{1}{100}$,$b=130$
$x=-\frac{b}{2a}=-\frac{130}{2×(-\frac{1}{100})}=6500$
即当$x = 6500$时,$w_{内}$最大
$w_{内最大值}=\frac{4ac - b^{2}}{4a}=\frac{4×(-\frac{1}{100})×(-62500)-130^{2}}{4×(-\frac{1}{100})}=422500$
对于$w_{外}=-\frac{1}{100}x^{2}+(150 - a)x$,$a=-\frac{1}{100}$,$b=(150 - a)$,$c = 0$
$w_{外最大值}=\frac{4ac - b^{2}}{4a}=\frac{0-(150 - a)^{2}}{4×(-\frac{1}{100})}=25(150 - a)^{2}$
由题意得$25(150 - a)^{2}=422500$
$(150 - a)^{2}=16900$
$150 - a=\pm130$
$a = 150\pm130$
$a_{1}=20$(舍去),$a_{2}=30$
即$a = 30$
$x=-\frac{b}{2a}=-\frac{130}{2×(-\frac{1}{100})}=6500$
即当$x = 6500$时,$w_{内}$最大
$w_{内最大值}=\frac{4ac - b^{2}}{4a}=\frac{4×(-\frac{1}{100})×(-62500)-130^{2}}{4×(-\frac{1}{100})}=422500$
对于$w_{外}=-\frac{1}{100}x^{2}+(150 - a)x$,$a=-\frac{1}{100}$,$b=(150 - a)$,$c = 0$
$w_{外最大值}=\frac{4ac - b^{2}}{4a}=\frac{0-(150 - a)^{2}}{4×(-\frac{1}{100})}=25(150 - a)^{2}$
由题意得$25(150 - a)^{2}=422500$
$(150 - a)^{2}=16900$
$150 - a=\pm130$
$a = 150\pm130$
$a_{1}=20$(舍去),$a_{2}=30$
即$a = 30$
(4)如果某月要将5000件产品全部销售完,请你通过分析帮公司决策,选择在国内还是在国外销售才能使所获月利润较大?
解:当$x = 5000$时
$w_{内}=-\frac{1}{100}×5000^{2}+130×5000 - 62500=337500$
$w_{外}=-\frac{1}{100}×5000^{2}+(150 - a)×5000=-5000a + 500000$
当$w_{内}>w_{外}$时,$337500>-5000a + 500000$,$a>32.5$
当$w_{内}=w_{外}$时,$337500=-5000a + 500000$,$a = 32.5$
当$w_{内}<w_{外}$时,$337500<-5000a + 500000$,$a<32.5$
$\because10\leq a\leq40$
$\therefore$当$10\leq a<32.5$时,选择国外销售;当$a = 32.5$时,国内外销售利润相同;当$32.5<a\leq40$时,选择国内销售
$w_{内}=-\frac{1}{100}×5000^{2}+130×5000 - 62500=337500$
$w_{外}=-\frac{1}{100}×5000^{2}+(150 - a)×5000=-5000a + 500000$
当$w_{内}>w_{外}$时,$337500>-5000a + 500000$,$a>32.5$
当$w_{内}=w_{外}$时,$337500=-5000a + 500000$,$a = 32.5$
当$w_{内}<w_{外}$时,$337500<-5000a + 500000$,$a<32.5$
$\because10\leq a\leq40$
$\therefore$当$10\leq a<32.5$时,选择国外销售;当$a = 32.5$时,国内外销售利润相同;当$32.5<a\leq40$时,选择国内销售
答案:
思路导引:解答此类题的关键是建立二次函数的模型,基本思路为:①理解题意,列出函数解析式;②根据函数解析式,结合图象的性质求解;③检验结果的合理性,得出实际问题的答案。
解:
(1)140 57500
(2)$w_{内} = x(y - 20) - 62500 = -\frac{1}{100}x^2 + 130x - 62500$,$w_{外} = -\frac{1}{100}x^2 + (150 - a)x$。
(3)当$x = -\frac{130}{2 × (-\frac{1}{100})} = 6500$时,$w_{内}$最大。由题意,得$\frac{0 - (150 - a)^2}{4 × (-\frac{1}{100})} = \frac{4 × (-\frac{1}{100}) × (-62500) - 130^2}{4 × (-\frac{1}{100})}$。
解得$a_1 = 30$,$a_2 = 270$(不合题意,舍去)。因此$a = 30$。
(4)当$x = 5000$时,$w_{内} = 337500$,$w_{外} = -5000a + 500000$。
若$w_{内} < w_{外}$,则$a < 32.5$;
若$w_{内} = w_{外}$,则$a = 32.5$;
若$w_{内} > w_{外}$,则$a > 32.5$。
$\therefore当10 \leq a < 32.5$时,选择在国外销售;
当$a = 32.5$时,在国外和国内销售都一样;
当$32.5 < a \leq 40$时,选择在国内销售。
解:
(1)140 57500
(2)$w_{内} = x(y - 20) - 62500 = -\frac{1}{100}x^2 + 130x - 62500$,$w_{外} = -\frac{1}{100}x^2 + (150 - a)x$。
(3)当$x = -\frac{130}{2 × (-\frac{1}{100})} = 6500$时,$w_{内}$最大。由题意,得$\frac{0 - (150 - a)^2}{4 × (-\frac{1}{100})} = \frac{4 × (-\frac{1}{100}) × (-62500) - 130^2}{4 × (-\frac{1}{100})}$。
解得$a_1 = 30$,$a_2 = 270$(不合题意,舍去)。因此$a = 30$。
(4)当$x = 5000$时,$w_{内} = 337500$,$w_{外} = -5000a + 500000$。
若$w_{内} < w_{外}$,则$a < 32.5$;
若$w_{内} = w_{外}$,则$a = 32.5$;
若$w_{内} > w_{外}$,则$a > 32.5$。
$\therefore当10 \leq a < 32.5$时,选择在国外销售;
当$a = 32.5$时,在国外和国内销售都一样;
当$32.5 < a \leq 40$时,选择在国内销售。
查看更多完整答案,请扫码查看


