《2025年全效学习课时提优九年级数学全一册人教版精华版》

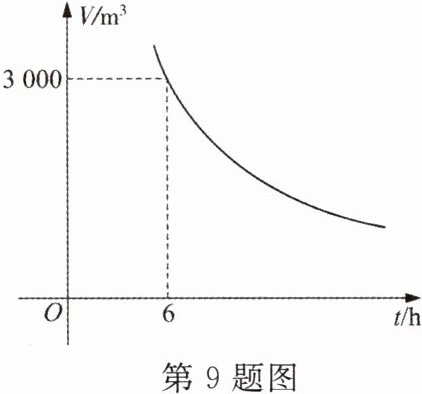
9. 工作人员对一蓄水池进行排水,每小时的排水量V(单位：$m^3)$与排完水池中的水所用的时间t(单位：h)之间满足如图所示的反比例函数关系.
(1)该蓄水池的蓄水量为$$18000$$$m^3；$
(2)如果每小时排水量不超过$2000 m^3,$那么排完水池中的水所用的时间t满足的条件是$t\geqslant9$；
(3)由于该工作人员有其他任务,为了提前2小时排完水池中的水,需将原计划每小时的排水量增加25%,则原计划每小时的排水量为$$1800$$$m^3.$

答案：
(1)18 000
(2)$t\geqslant9$
(3)1 800

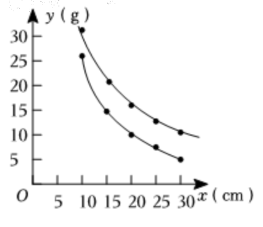
10. 在实验课上,小明做了一个试验. 如图1,在仪器左边托盘A(固定)中放置一个物体,在右边托盘B(可左右移动)中放置一个可以装水的容器,容器的质量为5 g. 在容器中加入一定质量的水,可以使仪器左右平衡. 改变托盘B与点C的距离x(单位：cm)(0＜x≤60),记录容器中加入的水的质量,得到下表：
把上表中的x与$y_1$各组对应值作为点的坐标,在平面直角坐标系中描出这些点,并用光滑的曲线连接起来,得到如图2所示的$y_1$关于x的函数图象.
(1)请在该平面直角坐标系中作出$y_2$关于x的函数图象；
(2)观察函数图象,并结合表中的数据：
①猜测$y_1$与x之间的函数关系,并求$y_1$关于x的函数解析式；
②求$y_2$关于x的函数解析式；
③当0＜x≤60时$,y_1$随x的增大而______(填“增大”或“减小”),$y_2$随x的增大而______(填“增大”或“减小”),$y_2$的图象可以由$y_1$的图象向______(填“上”或“下”或“左”或“右”)平移得到；
(3)若在容器中加入的水的质量$y_2$满足$19≤y_2≤45,$求托盘B与点C的距离x的取值范围.
(1)略
(2)①$y_1=$$\frac{300}{x}$ ②$y_2=$$\frac{300}{x}-5$ ③减小 减小 下
(3)$6\leqslant x\leqslant12.5$

答案：

(1)如图所示

(2)①$y_1=\frac{300}{x}$ ②$y_2=\frac{300}{x}-5$ ③减小 减小 下
(3)$6\leqslant x\leqslant12.5$

11. [模型观念]某次科学实验中,记录员对两个变量(都大于或等于0)记录了一些数据,如下表.
 

他将以上数据分两部分,抽象成两个函数模型：y= kx+b(k≠0),y= m/x(m≠0).
(1)在图中描出表中数据对应的点,求出两部分的函数解析式,并画出两部分的函数图象；
(2)当y≥1时,求x的取值范围.

答案：

(1)$y=2x$,$y=\frac{8}{x}$,如图所示

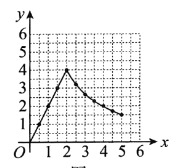
(2)$\frac{1}{2}\leqslant x\leqslant8$