《2025年全效学习课时提优九年级数学全一册人教版精华版》

7. 生产季节性产品的企业,当它的产品无利润时就会及时停产. 现有一生产季节性产品的企业,若其一年中获得的利润y(单位：元)和月份n之间的函数解析式为$y= -n^2 + 14n - 24$(n是整数,$0 ＜ n\leq12$),则该企业一年中应停产的月份是(C)
A.1月、2月、3月
B.2月、3月、4月
C.1月、2月、12月
D.1月、11月、12月

答案： C

8. 某水果店销售某种水果,由历年市场行情可知,从1月至12月,这种水果每千克售价$y_1$(单位：元)与销售月份x之间存在如图1所示的变化趋势,每千克成本$y_2$(单位：元)与销售月份x满足函数关系式$y_2= mx^2 - 8mx + n$,其变化趋势如图2所示.

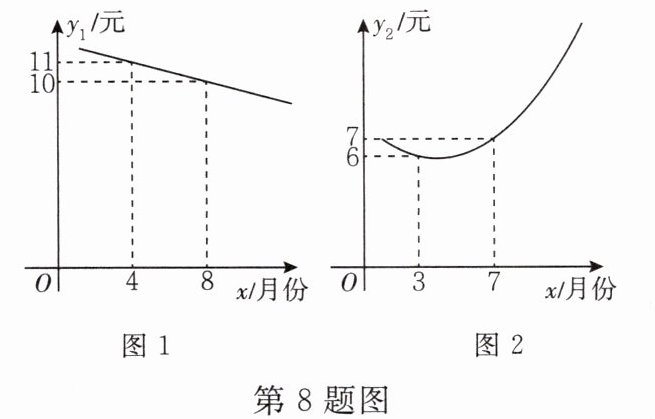
(1)求$y_2$的函数解析式(不要求写出自变量的取值范围)；
(2)几月销售这种水果每千克所获得的利润最大？最大利润是多少？

答案：
(1)$y_{2}=\frac {1}{8}x^{2}-x+\frac {63}{8}$
(2)3月,5.25元

9. [应用意识]某文具店最近有A,B两款纪念册比较畅销,该店购进A款纪念册5本和B款纪念册4本共需156元；购进A款纪念册3本和B款纪念册5本共需130元. 在销售中发现：A款纪念册售价为32元/本时,每天的销售量为40本,每降低1元可多售出2本；B款纪念册售价为22元/本时,每天的销售量为80本,B款纪念册每天的销售量与售价之间满足一次函数关系,其部分对应数据如下表所示：
 

(1)求A,B两款纪念册每本的进价分别为多少元；
(2)该店准备降低A款纪念册每本的售价,同时提高B款纪念册每本的售价,且保证这两款纪念册每天销售总数不变,设每件A类特产降价x元,该店每天销售这两类特产的总利润为w元,求w与x的函数关系式,并求出A类特产每件降价多少元时,总利润w最大,最大利润是多少元？
①直接写出B款纪念册每天的销售量(用含m的代数式表示)；
②当A款纪念册售价为多少元时,该店每天所获利润最大？最大利润是多少？

答案：
(1)20元和14元
(2)①$(80-2m)$本 ②26元,1264元