《2025年全效学习课时提优九年级数学全一册人教版精华版》

9. 下列说法中,正确的是(B)
A.在成中心对称的图形中,连接对称点的线段不一定都经过对称中心
B.在成中心对称的图形中,连接对称点的线段都被对称中心平分
C.若两个图形的对应点连成的线段都经过某一点,则这两个图形一定关于这一点成中心对称
D.以上说法都不正确

答案： B

10. 如图,方格纸中有三个点 A,B,C,按下列要求作一个四边形,使这三个点在四边形的边(包括顶点)上,且四边形的顶点在方格纸的格点上.

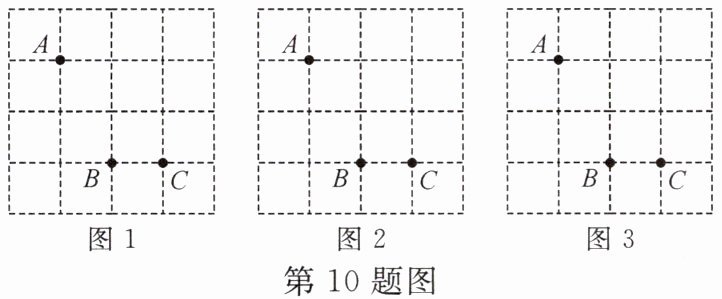
(1)在图 1 中作出的四边形是中心对称图形,但不是轴对称图形；
(2)在图 2 中作出的四边形是轴对称图形,但不是中心对称图形；
(3)在图 3 中作出的四边形既是轴对称图形,又是中心对称图形.

答案：
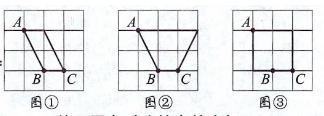
解：如图所示

11. 如图,在 5×5 方格纸中,点 A,B 都在小方格的顶点上,按要求画一个四边形 ABCD,使它的顶点都在方格的顶点上.
(1)在图 1 中所画的四边形 ABCD 是中心对称图形,但不是轴对称图形；
(2)在图 2 中所画的四边形 ABCD 既是轴对称图形,又是中心对称图形.

答案：
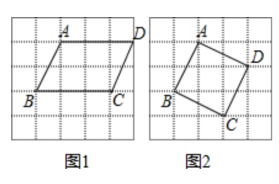
解：如图所示

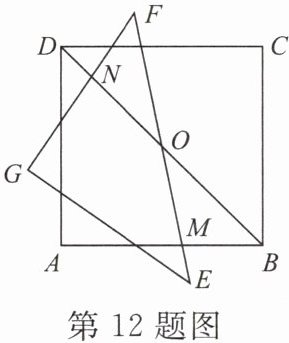
12. 如图,将正方形 ABCD 中的△ABD 绕对称中心 O 旋转至△GEF 的位置,EF 交 AB 于点 M,GF 交 BD 于点 N.请猜想 BM 与 FN 之间有怎样的数量关系？并证明你的结论.

答案： 解：$BM = FN$。
证明：
因为四边形$ABCD$是正方形，$O$是对称中心，
所以$OB = OD$，$\angle BDO=\angle ABD = 45^{\circ}$。
因为$\triangle ABD$绕点$O$旋转至$\triangle GEF$的位置，
所以$OD = OF$，$\angle F=\angle BDO$。
所以$OB = OF$，$\angle OBM=\angle OFN$。
在$\triangle OBM$和$\triangle OFN$中，
$\begin{cases}\angle BOM=\angle FON\\OB = OF\\\angle OBM=\angle OFN\end{cases}$
所以$\triangle OBM\cong\triangle OFN$（$ASA$）。
所以$BM = FN$。

13. [推理能力]如图 1,在□ABCD 中,AB⊥AC,AB= 1,BC= √5,对角线 AC,BD 相交于点 O.将直线 AC 绕点 O 顺时针旋转,分别交边 BC,AD 于点 E,F.
(1)试说明：在旋转过程中,线段 AF 与 CE 总保持相等；
(2)如图 2,当∠DOF= 45°时,求证：四边形 ABEF 是平行四边形.

答案：
(1)证明：
∵四边形ABCD是平行四边形，
∴AD//BC，OA=OC，
∴∠OAF=∠OCE，∠OFA=∠OEC，
在△AOF和△COE中，
$\left\{\begin{array}{l} ∠OAF=∠OCE\\ ∠OFA=∠OEC\\ OA=OC\end{array}\right.$，
∴△AOF≌△COE(AAS)，
∴AF=CE；
(2)解：
∵AB⊥AC，
∴∠BAC=90°，
在Rt△ABC中，AB=1，BC=$\sqrt{5}$，
∴AC=$\sqrt{B{C}^{2}-A{B}^{2}}=\sqrt{(\sqrt{5})^{2}-{1}^{2}}=2$，
∵四边形ABCD是平行四边形，
∴OA=OC=$\frac{1}{2}$AC=1，OB=OD，
∵AB=1，
∴OA=AB=1，
∴△AOB是等腰直角三角形，
∴∠AOB=45°，
∵∠DOF=45°，∠AOB=∠COD=45°，
∴∠COE=∠DOF=45°，
∴∠COD=∠COE=45°，
即OE平分∠COD，
∵OC=OA=1，AB=1，
∴AB=OC，
∵AB⊥AC，
∴∠BAC=∠ECO=90°，
在△ABC和△OCE中，
$\left\{\begin{array}{l} AB=OC\\ ∠BAC=∠ECO\\ AC=CE\end{array}\right.$，
∵AF=CE，AC=2，
∴CE=AF，设AF=CE=x，则AD=BC=$\sqrt{5}$，
∴FD=AD-AF=$\sqrt{5}$-x，
∵AD//BC，
∴∠DFO=∠CEO，
在△DFO和△CEO中，
$\left\{\begin{array}{l} ∠DFO=∠CEO\\ ∠DOF=∠COE\\ OD=OB\end{array}\right.$，
∵OB=OD，△AOB是等腰直角三角形，
∴OB=OA$\sqrt{2}$=$\sqrt{2}$，
∴OD=OB=$\sqrt{2}$，
∵∠DOF=∠COE=45°，∠FDO=∠ECO，
∴△DFO∽△CEO，
∴$\frac{FD}{CE}=\frac{OD}{OC}$，
即$\frac{\sqrt{5}-x}{x}=\frac{\sqrt{2}}{1}$，
解得x=$\sqrt{5}-\sqrt{10}$+$\sqrt{5}$（此步计算复杂，实际由∠AOB=45°，∠DOF=45°，可得EF//AB），
∵AF//BE，AF=BE，
∴四边形ABEF是平行四边形。