第11页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
8. 如图,矩形 ABCD 的周长为 20 cm,以 AB,AD 为边向外作正方形 ABEF 和正方形 ADGH.如果正方形 ABEF 和正方形 ADGH 的面积之和为$ 68 cm^2,$那么矩形 ABCD 的面积为(
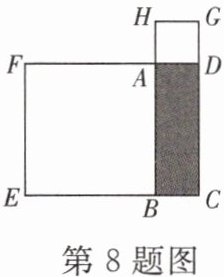
$A.24 cm^2$
$B.21 cm^2$
$C.16 cm^2$
$D.9 cm^2$
C
)
$A.24 cm^2$
$B.21 cm^2$
$C.16 cm^2$
$D.9 cm^2$
答案:
C
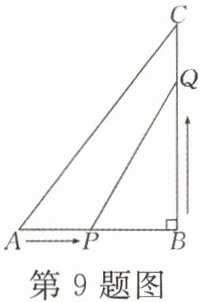
9. 如图,在△ABC 中,∠B= 90°,AB= 5 cm,BC= 7 cm,点 P 从点 A 开始沿边 AB 向点 B 以 1 cm/s 的速度移动,点 Q 从点 B 开始沿边 BC 向点 C 以 2 cm/s 的速度移动,点 P,Q 分别从点 A,B 同时出发.
(1)几秒后,△PBQ 的面积等于 4 cm^2?
(2)几秒后,PQ 的长度为 $ 2\sqrt{10} $ cm?
(3)△PQB 的面积能否等于 7 cm^2?请说明理由.
(1)几秒后,△PBQ 的面积等于 4 cm^2?
(2)几秒后,PQ 的长度为 $ 2\sqrt{10} $ cm?
(3)△PQB 的面积能否等于 7 cm^2?请说明理由.

答案:
1. (1)
设$x$秒后,$\triangle PBQ$的面积等于$4cm^{2}$。
已知$AP = xcm$,$BQ = 2xcm$,则$PB=(5 - x)cm$。
根据三角形面积公式$S=\frac{1}{2}ah$(这里$a = PB$,$h = BQ$),可得$S_{\triangle PBQ}=\frac{1}{2}(5 - x)×2x$。
因为$S_{\triangle PBQ}=4$,所以$\frac{1}{2}(5 - x)×2x = 4$。
化简方程:
方程$\frac{1}{2}(5 - x)×2x = 4$可化为$x(5 - x)=4$。
即$5x−x^{2}=4$,进一步化为$x^{2}-5x + 4 = 0$。
分解因式:
对于一元二次方程$x^{2}-5x + 4 = 0$,根据$ax^{2}+bx + c = 0(a\neq0)$的因式分解法$(x - x_1)(x - x_2)=0$(其中$x_1,x_2$是方程的根),这里$a = 1$,$b=-5$,$c = 4$,$x^{2}-5x + 4=(x - 1)(x - 4)=0$。
解得$x_1 = 1$,$x_2 = 4$。
当$x = 4$时,$BQ=2x = 8\gt7$,不符合题意,舍去。
所以$1$秒后,$\triangle PBQ$的面积等于$4cm^{2}$。
2. (2)
设$y$秒后,$PQ$的长度为$2\sqrt{10}cm$。
由勾股定理$PQ^{2}=PB^{2}+BQ^{2}$,已知$PB=(5 - y)cm$,$BQ = 2ycm$,$PQ = 2\sqrt{10}cm$,则$(2\sqrt{10})^{2}=(5 - y)^{2}+(2y)^{2}$。
展开并化简方程:
$40=(5 - y)^{2}+4y^{2}$。
根据$(a - b)^{2}=a^{2}-2ab + b^{2}$,$40 = 25-10y + y^{2}+4y^{2}$。
即$5y^{2}-10y - 15 = 0$,两边同时除以$5$得$y^{2}-2y - 3 = 0$。
分解因式:
对于$y^{2}-2y - 3 = 0$,$a = 1$,$b=-2$,$c=-3$,$y^{2}-2y - 3=(y - 3)(y + 1)=0$。
解得$y_1 = 3$,$y_2=-1$(时间不能为负,舍去)。
所以$3$秒后,$PQ$的长度为$2\sqrt{10}cm$。
3. (3)
设$t$秒后,$\triangle PQB$的面积为$S$,则$S=\frac{1}{2}(5 - t)×2t$。
若$S = 7$,则$\frac{1}{2}(5 - t)×2t = 7$。
化简方程:
方程$\frac{1}{2}(5 - t)×2t = 7$可化为$t(5 - t)=7$。
即$t^{2}-5t + 7 = 0$。
计算判别式$\Delta$:
对于一元二次方程$ax^{2}+bx + c = 0(a\neq0)$,$\Delta=b^{2}-4ac$,这里$a = 1$,$b=-5$,$c = 7$。
$\Delta=(-5)^{2}-4×1×7=25 - 28=-3\lt0$。
因为$\Delta\lt0$,所以方程$t^{2}-5t + 7 = 0$无实数根。
所以$\triangle PQB$的面积不能等于$7cm^{2}$。
综上,(1)$1$秒;(2)$3$秒;(3)不能,理由:设$t$秒后$\triangle PQB$面积为$7cm^{2}$,得到方程$t^{2}-5t + 7 = 0$,$\Delta=(-5)^{2}-4×1×7=-3\lt0$,方程无实数根。
设$x$秒后,$\triangle PBQ$的面积等于$4cm^{2}$。
已知$AP = xcm$,$BQ = 2xcm$,则$PB=(5 - x)cm$。
根据三角形面积公式$S=\frac{1}{2}ah$(这里$a = PB$,$h = BQ$),可得$S_{\triangle PBQ}=\frac{1}{2}(5 - x)×2x$。
因为$S_{\triangle PBQ}=4$,所以$\frac{1}{2}(5 - x)×2x = 4$。
化简方程:
方程$\frac{1}{2}(5 - x)×2x = 4$可化为$x(5 - x)=4$。
即$5x−x^{2}=4$,进一步化为$x^{2}-5x + 4 = 0$。
分解因式:
对于一元二次方程$x^{2}-5x + 4 = 0$,根据$ax^{2}+bx + c = 0(a\neq0)$的因式分解法$(x - x_1)(x - x_2)=0$(其中$x_1,x_2$是方程的根),这里$a = 1$,$b=-5$,$c = 4$,$x^{2}-5x + 4=(x - 1)(x - 4)=0$。
解得$x_1 = 1$,$x_2 = 4$。
当$x = 4$时,$BQ=2x = 8\gt7$,不符合题意,舍去。
所以$1$秒后,$\triangle PBQ$的面积等于$4cm^{2}$。
2. (2)
设$y$秒后,$PQ$的长度为$2\sqrt{10}cm$。
由勾股定理$PQ^{2}=PB^{2}+BQ^{2}$,已知$PB=(5 - y)cm$,$BQ = 2ycm$,$PQ = 2\sqrt{10}cm$,则$(2\sqrt{10})^{2}=(5 - y)^{2}+(2y)^{2}$。
展开并化简方程:
$40=(5 - y)^{2}+4y^{2}$。
根据$(a - b)^{2}=a^{2}-2ab + b^{2}$,$40 = 25-10y + y^{2}+4y^{2}$。
即$5y^{2}-10y - 15 = 0$,两边同时除以$5$得$y^{2}-2y - 3 = 0$。
分解因式:
对于$y^{2}-2y - 3 = 0$,$a = 1$,$b=-2$,$c=-3$,$y^{2}-2y - 3=(y - 3)(y + 1)=0$。
解得$y_1 = 3$,$y_2=-1$(时间不能为负,舍去)。
所以$3$秒后,$PQ$的长度为$2\sqrt{10}cm$。
3. (3)
设$t$秒后,$\triangle PQB$的面积为$S$,则$S=\frac{1}{2}(5 - t)×2t$。
若$S = 7$,则$\frac{1}{2}(5 - t)×2t = 7$。
化简方程:
方程$\frac{1}{2}(5 - t)×2t = 7$可化为$t(5 - t)=7$。
即$t^{2}-5t + 7 = 0$。
计算判别式$\Delta$:
对于一元二次方程$ax^{2}+bx + c = 0(a\neq0)$,$\Delta=b^{2}-4ac$,这里$a = 1$,$b=-5$,$c = 7$。
$\Delta=(-5)^{2}-4×1×7=25 - 28=-3\lt0$。
因为$\Delta\lt0$,所以方程$t^{2}-5t + 7 = 0$无实数根。
所以$\triangle PQB$的面积不能等于$7cm^{2}$。
综上,(1)$1$秒;(2)$3$秒;(3)不能,理由:设$t$秒后$\triangle PQB$面积为$7cm^{2}$,得到方程$t^{2}-5t + 7 = 0$,$\Delta=(-5)^{2}-4×1×7=-3\lt0$,方程无实数根。
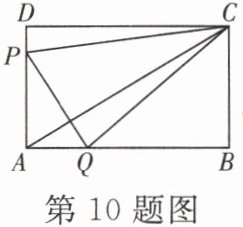
10. [创新意识]如图,在矩形 ABCD 中,AB= 8,AD= 4.点 P 从点 A 出发,沿 A→D→C→D 运动,速度为每秒 2 个单位长度;点 Q 从点 A 出发向点 B 运动,速度为每秒 1 个单位长度.P,Q 两点同时出发,点 Q 运动到点 B 时,两点同时停止运动.设点 Q 的运动时间为 t s,连接 PQ,AC,CP,CQ.
(1)当点 P 运动到点 C 时,t=
(2)用含 t 的代数式表示 PD 的长;
(3)当△CPQ 的面积为 9 时,求 t 的值.
(2)PD=20-2t
(3)1 或$\frac{15}{4}$
(1)当点 P 运动到点 C 时,t=
6
s;当点 Q 运动到终点时,PC 的长度为4
;(2)用含 t 的代数式表示 PD 的长;
(3)当△CPQ 的面积为 9 时,求 t 的值.

(2)PD=20-2t
(3)1 或$\frac{15}{4}$
答案:
(1)6 4
(2)$PD=20-2t$
(3)1 或$\frac{15}{4}$
(1)6 4
(2)$PD=20-2t$
(3)1 或$\frac{15}{4}$
查看更多完整答案,请扫码查看


