第10页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
1. 学校准备建一个面积为$ 375 m^2 $的矩形游泳池,且游泳池的宽比长短 10 m,求游泳池的长.若设游泳池的长为 x m,则可列方程为(
A.$ x(x-10)= 375 $
B.$ x(x+10)= 375 $
C.$ 2x(2x-10)= 375 $
D.$ 2x(2x+10)= 375 $
A
)A.$ x(x-10)= 375 $
B.$ x(x+10)= 375 $
C.$ 2x(2x-10)= 375 $
D.$ 2x(2x+10)= 375 $
答案:
A
2. 公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了 1 m,另一边减少了 2 m,剩余空地的面积为$ 18 m^2,$求原正方形空地的边长.设原正方形空地的边长为 x m,则可列方程为 (
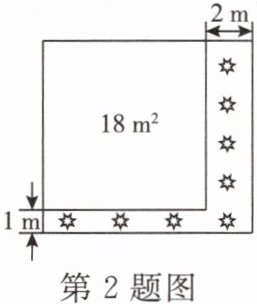
A.$ (x+1)(x+2)= 18 $
B.$ x^2-3x+16= 0 $
C.$ (x-1)(x-2)= 18 $
D.$ x^2+3x+16= 0 $
C
)
A.$ (x+1)(x+2)= 18 $
B.$ x^2-3x+16= 0 $
C.$ (x-1)(x-2)= 18 $
D.$ x^2+3x+16= 0 $
答案:
C
3. 如图,某小区要在长为 16 m、宽为 12 m 的矩形空地上建造一个花坛,使花坛四周小路的宽度相等,且花坛所占面积为空地面积的一半,则小路的宽为
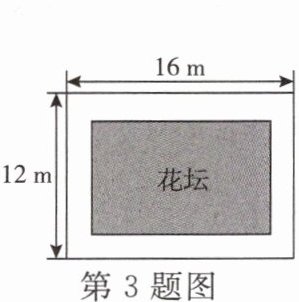
2
m.
答案:
2
4. 在 20 世纪 70 年代,我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”,在全国大规模推广,取得了很大成果.如图,利用黄金分割法作 EF 将矩形窗框 ABCD 分为上、下两部分,其中 E 为边 AB 的黄金分割点,即 $ BE^2= AE·AB $.已知 AB 的长为 2 m,则线段 BE 的长为
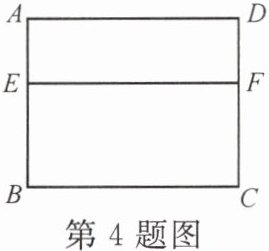
$\sqrt{5}-1$
m.
答案:
$\sqrt{5}-1$
5. 如图是一张长为 12 cm、宽为 10 cm 的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形,剩余部分(阴影部分)可制成底面积为$ 24 cm^2 $的有盖的长方体铁盒,则剪去的正方形的边长为
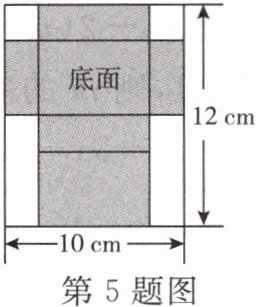
2
cm.
答案:
2
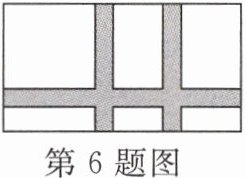
6. 如图,要在 20 m 宽、32 m 长的矩形耕地上修筑同样宽的三条小路(两条纵向,一条横向,横向与纵向互相垂直),把耕地分成大小不等的六块花田,要使花田面积为$ 570 m^2,$则道路应修多宽?

答案:
1 m
7. 如图,老李想用长为 70 m 的栅栏,再借助房屋的外墙(外墙足够长)围成一个矩形羊圈 ABCD,并在边 BC 上留一个 2 m 宽的门(建在 EF 处,另用其他材料).
(1)当羊圈的长和宽分别为多少米时,能围成一个面积为$ 640 m^2 $的羊圈?
(2)羊圈的面积能达到$ 650 m^2 $吗?如果能,请你给出设计方案;如果不能,请说明理由.

(1)当羊圈的长和宽分别为多少米时,能围成一个面积为$ 640 m^2 $的羊圈?
(2)羊圈的面积能达到$ 650 m^2 $吗?如果能,请你给出设计方案;如果不能,请说明理由.

答案:
1. (1)
设羊圈的宽$AB = xm$,则长$BC=(70 + 2-2x)m=(72 - 2x)m$。
根据矩形面积公式$S = AB× BC$,已知$S = 640m^{2}$,可得方程:
$x(72 - 2x)=640$。
展开方程得$72x-2x^{2}=640$。
移项化为标准的一元二次方程形式$2x^{2}-72x + 640 = 0$,两边同时除以$2$得$x^{2}-36x + 320 = 0$。
对于一元二次方程$ax^{2}+bx + c = 0(a\neq0)$,这里$a = 1$,$b=-36$,$c = 320$,根据求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$,先计算判别式$\Delta=b^{2}-4ac=(-36)^{2}-4×1×320=1296 - 1280 = 16$。
则$x=\frac{36\pm\sqrt{16}}{2}=\frac{36\pm4}{2}$。
当$x=\frac{36 + 4}{2}$时,$x_{1}=\frac{40}{2}=20$;当$x=\frac{36-4}{2}$时,$x_{2}=\frac{32}{2}=16$。
当$x = 20$时,$BC=72-2x=72-2×20 = 32$;当$x = 16$时,$BC=72-2x=72-2×16 = 40$。
所以当长为$32m$,宽为$20m$或长为$40m$,宽为$16m$时,能围成面积为$640m^{2}$的羊圈。
2. (2)
设羊圈面积为$y m^{2}$,$AB = xm$,则$y=x(72 - 2x)$。
展开得$y=-2x^{2}+72x$,对于二次函数$y = ax^{2}+bx + c(a\neq0)$,这里$a=-2$,$b = 72$,$c = 0$,其对称轴为$x=-\frac{b}{2a}=-\frac{72}{2×(-2)} = 18$,函数的最大值为$y=-2×18^{2}+72×18$。
先计算$y=-2×324+1296=-648 + 1296 = 648$。
另一种方法:假设$x(72 - 2x)=650$,即$2x^{2}-72x + 650 = 0$,$x^{2}-36x + 325 = 0$。
对于一元二次方程$ax^{2}+bx + c = 0(a = 1$,$b=-36$,$c = 325)$,判别式$\Delta=b^{2}-4ac=(-36)^{2}-4×1×325=1296 - 1300=-4\lt0$。
因为二次函数$y=-2x^{2}+72x$的最大值$y = 648\lt650$,且方程$x(72 - 2x)=650$无实数根。
所以:
(1) 长为$32m$,宽为$20m$或长为$40m$,宽为$16m$;
(2) 羊圈的面积不能达到$650m^{2}$,因为方程$x(72 - 2x)=650$无实数根(或二次函数$y=-2x^{2}+72x$的最大值小于$650$)。
设羊圈的宽$AB = xm$,则长$BC=(70 + 2-2x)m=(72 - 2x)m$。
根据矩形面积公式$S = AB× BC$,已知$S = 640m^{2}$,可得方程:
$x(72 - 2x)=640$。
展开方程得$72x-2x^{2}=640$。
移项化为标准的一元二次方程形式$2x^{2}-72x + 640 = 0$,两边同时除以$2$得$x^{2}-36x + 320 = 0$。
对于一元二次方程$ax^{2}+bx + c = 0(a\neq0)$,这里$a = 1$,$b=-36$,$c = 320$,根据求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$,先计算判别式$\Delta=b^{2}-4ac=(-36)^{2}-4×1×320=1296 - 1280 = 16$。
则$x=\frac{36\pm\sqrt{16}}{2}=\frac{36\pm4}{2}$。
当$x=\frac{36 + 4}{2}$时,$x_{1}=\frac{40}{2}=20$;当$x=\frac{36-4}{2}$时,$x_{2}=\frac{32}{2}=16$。
当$x = 20$时,$BC=72-2x=72-2×20 = 32$;当$x = 16$时,$BC=72-2x=72-2×16 = 40$。
所以当长为$32m$,宽为$20m$或长为$40m$,宽为$16m$时,能围成面积为$640m^{2}$的羊圈。
2. (2)
设羊圈面积为$y m^{2}$,$AB = xm$,则$y=x(72 - 2x)$。
展开得$y=-2x^{2}+72x$,对于二次函数$y = ax^{2}+bx + c(a\neq0)$,这里$a=-2$,$b = 72$,$c = 0$,其对称轴为$x=-\frac{b}{2a}=-\frac{72}{2×(-2)} = 18$,函数的最大值为$y=-2×18^{2}+72×18$。
先计算$y=-2×324+1296=-648 + 1296 = 648$。
另一种方法:假设$x(72 - 2x)=650$,即$2x^{2}-72x + 650 = 0$,$x^{2}-36x + 325 = 0$。
对于一元二次方程$ax^{2}+bx + c = 0(a = 1$,$b=-36$,$c = 325)$,判别式$\Delta=b^{2}-4ac=(-36)^{2}-4×1×325=1296 - 1300=-4\lt0$。
因为二次函数$y=-2x^{2}+72x$的最大值$y = 648\lt650$,且方程$x(72 - 2x)=650$无实数根。
所以:
(1) 长为$32m$,宽为$20m$或长为$40m$,宽为$16m$;
(2) 羊圈的面积不能达到$650m^{2}$,因为方程$x(72 - 2x)=650$无实数根(或二次函数$y=-2x^{2}+72x$的最大值小于$650$)。
查看更多完整答案,请扫码查看


