《2025年全效学习课时提优九年级数学全一册人教版精华版》

1. △ABC在平面直角坐标系中的位置如图所示：
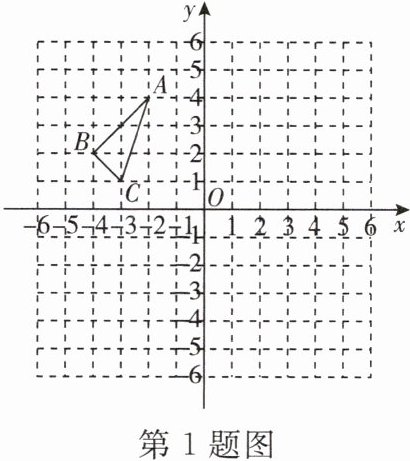
(1)画出△ABC关于原点对称的△A1B1C1；
(2)将△ABC绕点C顺时针旋转90°得到△A2B2C,画出旋转后的△A2B2C,并求出点A2,B2的坐标.

答案：
解：如图所示　　

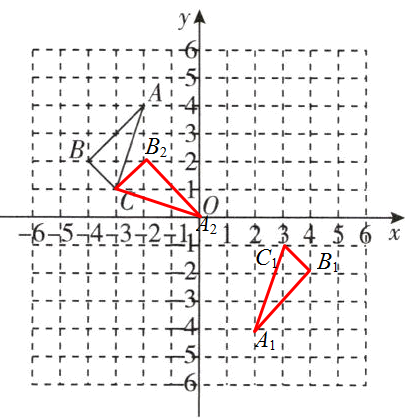
$A_2(0，$$0)、$$B_2(-2，$$2)$　　

2. 在4×4的方格纸中,请按下列要求画出格点三角形(顶点均在格点上).
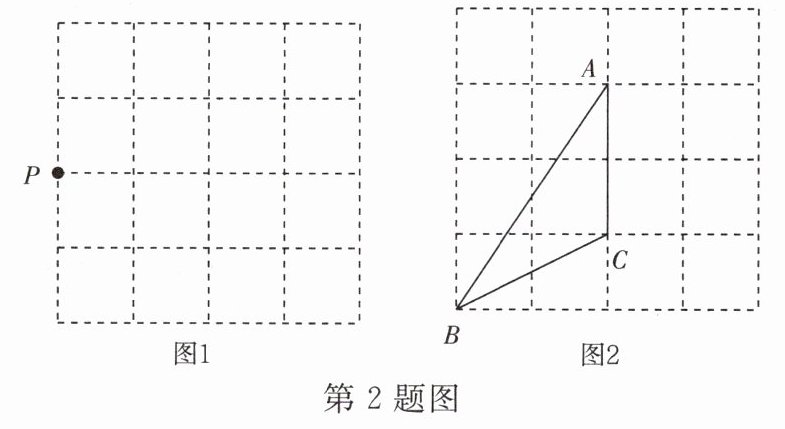
(1)在图1中先画出一个以格点P为顶点的等腰三角形PAB,再画出该三角形向右平移2个单位长度后的△P′A′B′；
(2)将图2中的格点三角形ABC绕点C按顺时针方向旋转90°,画出经旋转后的△A′B′C.

答案：
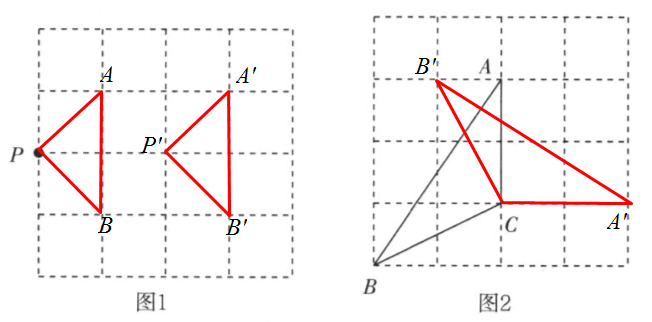
解：如图所示

3.【问题解决】
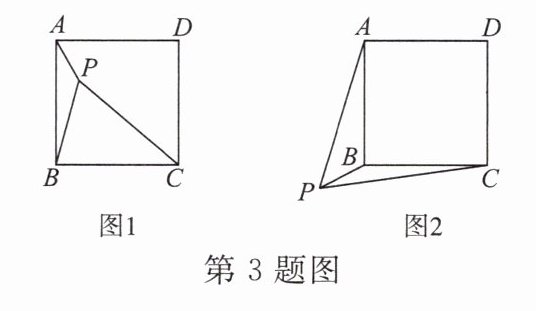
数学课上,老师提出了这样一个问题：如图1,P是正方形ABCD内一点,PA= 1,PB= 2,PC= 3,你能求出∠APB的度数吗？
小明通过观察、分析、思考,形成了如下思路：
思路一：将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,求出∠APB的度数；
思路二：将△APB绕点B顺时针旋转90°,得到△CP′B,连接PP′,求出∠APB的度数.
(1)请参考小明的思路,任选一种写出完整的解答过程；
【类比探究】
(2)如图2,若P是正方形ABCD外一点,PA= 3,PB= 1,PC= $\sqrt{11}$,求∠APB的度数.

答案：
(1)略
(2)$45^{\circ}$.

4. 如图1,△ABC和△CEF是两个大小不等的等边三角形,且有一个公共顶点C,连接AF和BE.
(1)线段AF和BE有怎样的大小关系？请证明你的结论；
(2)将图1中的△CEF绕点C旋转一定的角度,得到图2,(1)中的结论还成立吗？请说明理由.

答案： 1. （1）
解：$AF = BE$。
证明：
因为$\triangle ABC$和$\triangle CEF$是等边三角形，所以$AC = BC$，$CF = CE$，$\angle ACB=\angle FCE = 60^{\circ}$。
则$\angle ACB-\angle FCB=\angle FCE-\angle FCB$，即$\angle ACF=\angle BCE$。
在$\triangle ACF$和$\triangle BCE$中，$\begin{cases}AC = BC\\\angle ACF=\angle BCE\\CF = CE\end{cases}$。
根据$SAS$（边角边）定理，可得$\triangle ACF\cong\triangle BCE$。
所以$AF = BE$（全等三角形的对应边相等）。
2. （2）
解：$(1)$中的结论仍然成立。
理由：
因为$\triangle ABC$和$\triangle CEF$是等边三角形，所以$AC = BC$，$CF = CE$，$\angle ACB=\angle FCE = 60^{\circ}$。
$\angle ACB+\angle FCB=\angle FCE+\angle FCB$，即$\angle ACF=\angle BCE$。
在$\triangle ACF$和$\triangle BCE$中，$\begin{cases}AC = BC\\\angle ACF=\angle BCE\\CF = CE\end{cases}$。
根据$SAS$（边角边）定理，可得$\triangle ACF\cong\triangle BCE$。
所以$AF = BE$（全等三角形的对应边相等）。
综上，（1）$AF = BE$；（2）$(1)$中的结论成立。