第30页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
一 网格(坐标系)中的旋转作图
【教材母题1】(教材P62习题23.1第4题)
如图,分别画出△ABC绕点O逆时针旋转90°和180°后的图形.
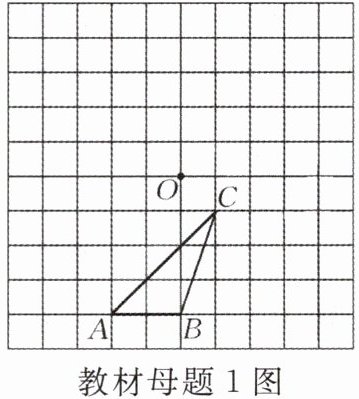
【思想方法】网格(坐标系)中旋转作图的一般步骤:①找出原图形中的关键点;②确定旋转中心、旋转角及旋转方向;③根据旋转的性质作出关键点的对应点;④按原图的关键点的连接顺序连接作出的点,并标上相应的字母.
【教材母题1】(教材P62习题23.1第4题)
如图,分别画出△ABC绕点O逆时针旋转90°和180°后的图形.

【思想方法】网格(坐标系)中旋转作图的一般步骤:①找出原图形中的关键点;②确定旋转中心、旋转角及旋转方向;③根据旋转的性质作出关键点的对应点;④按原图的关键点的连接顺序连接作出的点,并标上相应的字母.
答案:
解:如图所示
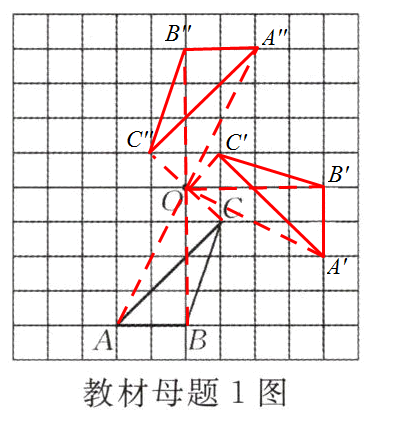
解:如图所示

【变式】(变网格中三角形为四边形)
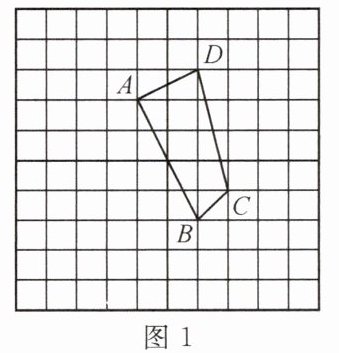
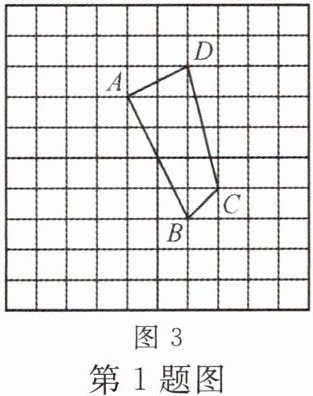
1. 如图,方格纸中每个小方格都是边长为1的正方形,我们把以格点连线为边的多边形称为“格点多边形”.如图1中四边形ABCD就是一个“格点四边形”.
(1)图1中四边形ABCD的面积为
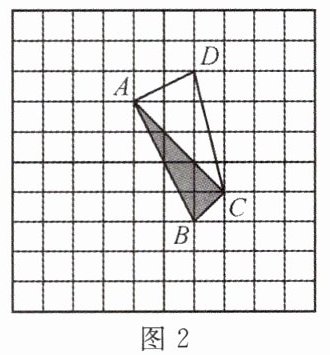
(2)在图2中,作出△ABC绕点B顺时针旋转90°后的△A′BC′;
(3)在图3中,画一个格点三角形BDE,使△BDE的面积等于四边形ABCD的面积且△BDE为轴对称图形(只需要作出1个即可).
(2)作图略
(3)作图略
1. 如图,方格纸中每个小方格都是边长为1的正方形,我们把以格点连线为边的多边形称为“格点多边形”.如图1中四边形ABCD就是一个“格点四边形”.
(1)图1中四边形ABCD的面积为
$\frac{15}{2}$
;(2)在图2中,作出△ABC绕点B顺时针旋转90°后的△A′BC′;
(3)在图3中,画一个格点三角形BDE,使△BDE的面积等于四边形ABCD的面积且△BDE为轴对称图形(只需要作出1个即可).



(2)作图略
(3)作图略
答案:
(1)$\frac{15}{2}$
(2)如图所示
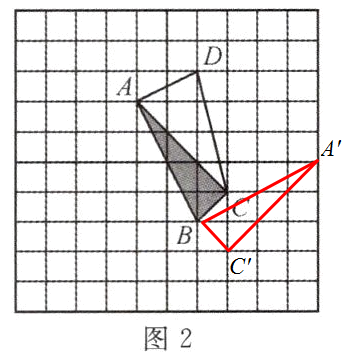
(3)如图所示
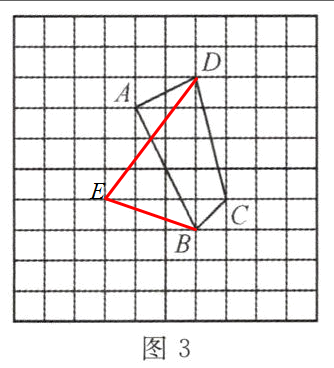
(1)$\frac{15}{2}$
(2)如图所示

(3)如图所示

二 旋转证明
【教材母题2】(教材P63习题23.1第10题)
如图,△ABD,△AEC都是等边三角形.BE与DC有什么关系?你能用旋转的性质说明上述关系成立的理由吗?
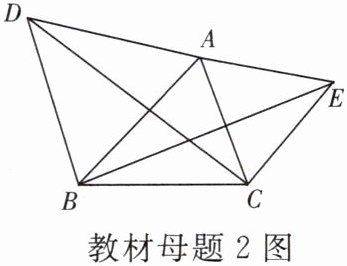
【思想方法】旋转前后的图形全等,借此可以在较复杂的图形中发现等量(或全等)关系,或通过旋转(割补)图形,把分散的已知量聚合起来,便于找到解题突破口,疏通解题思路.
【教材母题2】(教材P63习题23.1第10题)
如图,△ABD,△AEC都是等边三角形.BE与DC有什么关系?你能用旋转的性质说明上述关系成立的理由吗?

【思想方法】旋转前后的图形全等,借此可以在较复杂的图形中发现等量(或全等)关系,或通过旋转(割补)图形,把分散的已知量聚合起来,便于找到解题突破口,疏通解题思路.
答案:
1. 首先,根据等边三角形的性质:
因为$\triangle ABD$是等边三角形,所以$AD = AB$,$\angle BAD=60^{\circ}$;
因为$\triangle AEC$是等边三角形,所以$AE = AC$,$\angle CAE = 60^{\circ}$。
那么$\angle BAD+\angle BAC=\angle CAE+\angle BAC$。
2. 然后,得到角的关系:
即$\angle DAC=\angle BAE$。
3. 接着,利用全等三角形的判定定理($SAS$):
在$\triangle DAC$和$\triangle BAE$中,$\left\{\begin{array}{l}AD = AB\\\angle DAC=\angle BAE\\AC = AE\end{array}\right.$。
根据$SAS$(边角边)定理,可得$\triangle DAC\cong\triangle BAE$。
由全等三角形的性质可知$BE = DC$。
从旋转的性质来看:
把$\triangle ABE$绕点$A$逆时针旋转$60^{\circ}$,因为$AB = AD$,$AE = AC$,$\angle BAE=\angle DAC$,所以$AE$与$AC$重合,$AB$与$AD$重合。
即$\triangle ABE$绕点$A$逆时针旋转$60^{\circ}$后与$\triangle ADC$重合。
解:$BE = DC$。理由如下:
因为$\triangle ABD$和$\triangle AEC$都是等边三角形,所以$AD = AB$,$AC = AE$,$\angle BAD=\angle CAE = 60^{\circ}$。
所以$\angle BAD+\angle BAC=\angle CAE+\angle BAC$,即$\angle DAC=\angle BAE$。
在$\triangle DAC$和$\triangle BAE$中,$\left\{\begin{array}{l}AD = AB\\\angle DAC=\angle BAE\\AC = AE\end{array}\right.$,根据$SAS$定理$\triangle DAC\cong\triangle BAE$,所以$BE = DC$。
从旋转角度看,$\triangle ABE$绕点$A$逆时针旋转$60^{\circ}$可与$\triangle ADC$重合,根据旋转的性质(旋转前后的图形全等),所以$BE = DC$。
因为$\triangle ABD$是等边三角形,所以$AD = AB$,$\angle BAD=60^{\circ}$;
因为$\triangle AEC$是等边三角形,所以$AE = AC$,$\angle CAE = 60^{\circ}$。
那么$\angle BAD+\angle BAC=\angle CAE+\angle BAC$。
2. 然后,得到角的关系:
即$\angle DAC=\angle BAE$。
3. 接着,利用全等三角形的判定定理($SAS$):
在$\triangle DAC$和$\triangle BAE$中,$\left\{\begin{array}{l}AD = AB\\\angle DAC=\angle BAE\\AC = AE\end{array}\right.$。
根据$SAS$(边角边)定理,可得$\triangle DAC\cong\triangle BAE$。
由全等三角形的性质可知$BE = DC$。
从旋转的性质来看:
把$\triangle ABE$绕点$A$逆时针旋转$60^{\circ}$,因为$AB = AD$,$AE = AC$,$\angle BAE=\angle DAC$,所以$AE$与$AC$重合,$AB$与$AD$重合。
即$\triangle ABE$绕点$A$逆时针旋转$60^{\circ}$后与$\triangle ADC$重合。
解:$BE = DC$。理由如下:
因为$\triangle ABD$和$\triangle AEC$都是等边三角形,所以$AD = AB$,$AC = AE$,$\angle BAD=\angle CAE = 60^{\circ}$。
所以$\angle BAD+\angle BAC=\angle CAE+\angle BAC$,即$\angle DAC=\angle BAE$。
在$\triangle DAC$和$\triangle BAE$中,$\left\{\begin{array}{l}AD = AB\\\angle DAC=\angle BAE\\AC = AE\end{array}\right.$,根据$SAS$定理$\triangle DAC\cong\triangle BAE$,所以$BE = DC$。
从旋转角度看,$\triangle ABE$绕点$A$逆时针旋转$60^{\circ}$可与$\triangle ADC$重合,根据旋转的性质(旋转前后的图形全等),所以$BE = DC$。
【变式】(变条件中的等边三角形为等腰直角三角形)
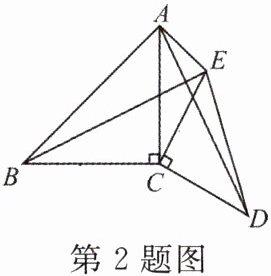
2. 如图,△ABC与△CDE都是等腰直角三角形,∠ACB= ∠DCE= 90°,AC= 6,点E在点A右侧,AE= 3,∠CAE= 45°.
(1)求证:△BCE≌△ACD;
(2)求AD的长.
2. 如图,△ABC与△CDE都是等腰直角三角形,∠ACB= ∠DCE= 90°,AC= 6,点E在点A右侧,AE= 3,∠CAE= 45°.
(1)求证:△BCE≌△ACD;
(2)求AD的长.

答案:
1. (1)证明:
因为$\angle ACB=\angle DCE = 90^{\circ}$,所以$\angle ACB+\angle ACE=\angle DCE+\angle ACE$,即$\angle BCE=\angle ACD$。
又因为$\triangle ABC$与$\triangle CDE$都是等腰直角三角形,$\angle ACB=\angle DCE = 90^{\circ}$,所以$BC = AC$,$CE = CD$。
在$\triangle BCE$和$\triangle ACD$中,$\begin{cases}BC = AC\\\angle BCE=\angle ACD\\CE = CD\end{cases}$,根据$SAS$(边角边)定理,可得$\triangle BCE\cong\triangle ACD$。
2. (2)
过点$E$作$EF\perp AC$于点$F$。
因为$\angle CAE = 45^{\circ}$,$\angle AFE = 90^{\circ}$,$AE = 3$,根据$\sin\angle CAE=\frac{EF}{AE}$,$\cos\angle CAE=\frac{AF}{AE}$,且$\sin45^{\circ}=\cos45^{\circ}=\frac{\sqrt{2}}{2}$,所以$EF = AF=AE\sin45^{\circ}=3×\frac{\sqrt{2}}{2}=\frac{3\sqrt{2}}{2}$。
已知$AC = 6$,则$CF=AC - AF=6-\frac{3\sqrt{2}}{2}$。
在$Rt\triangle CEF$中,根据勾股定理$CE^{2}=EF^{2}+CF^{2}$,$EF = AF=\frac{3\sqrt{2}}{2}$,$CF = 6-\frac{3\sqrt{2}}{2}$,则$CE^{2}=(\frac{3\sqrt{2}}{2})^{2}+(6 - \frac{3\sqrt{2}}{2})^{2}=\frac{9×2}{4}+36-2×6×\frac{3\sqrt{2}}{2}+\frac{9×2}{4}=9 + 36-18\sqrt{2}=45-18\sqrt{2}$。
因为$\triangle BCE\cong\triangle ACD$,所以$AD = BE$。
又因为$BC = AC = 6$,在$Rt\triangle BCE$中,根据勾股定理$BE^{2}=BC^{2}+CE^{2}$,$BC = 6$,$CE^{2}=45-18\sqrt{2}$,则$BE^{2}=36+(45 - 18\sqrt{2})=81-18\sqrt{2}$。
另一种方法:
因为$\triangle BCE\cong\triangle ACD$,所以$AD = BE$。
因为$\angle ACB=\angle DCE = 90^{\circ}$,$AC = BC = 6$,$\angle CAE = 45^{\circ}$,$\angle CAB = 45^{\circ}$,所以$\angle BAE=\angle BAC+\angle CAE=90^{\circ}$。
由$AC = 6$,$AE = 3$,根据勾股定理$BE=\sqrt{AB^{2}+AE^{2}}$,又因为$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{6^{2}+6^{2}}=\sqrt{72}=6\sqrt{2}$(等腰直角三角形三边关系$a:b:c = 1:1:\sqrt{2}$,这里$a = b = 6$,$c = AB$)。
所以$BE=\sqrt{(6\sqrt{2})^{2}+3^{2}}=\sqrt{72 + 9}=\sqrt{81}=9$。
所以(1)已证$\triangle BCE\cong\triangle ACD$;(2)$AD$的长为$9$。
因为$\angle ACB=\angle DCE = 90^{\circ}$,所以$\angle ACB+\angle ACE=\angle DCE+\angle ACE$,即$\angle BCE=\angle ACD$。
又因为$\triangle ABC$与$\triangle CDE$都是等腰直角三角形,$\angle ACB=\angle DCE = 90^{\circ}$,所以$BC = AC$,$CE = CD$。
在$\triangle BCE$和$\triangle ACD$中,$\begin{cases}BC = AC\\\angle BCE=\angle ACD\\CE = CD\end{cases}$,根据$SAS$(边角边)定理,可得$\triangle BCE\cong\triangle ACD$。
2. (2)
过点$E$作$EF\perp AC$于点$F$。
因为$\angle CAE = 45^{\circ}$,$\angle AFE = 90^{\circ}$,$AE = 3$,根据$\sin\angle CAE=\frac{EF}{AE}$,$\cos\angle CAE=\frac{AF}{AE}$,且$\sin45^{\circ}=\cos45^{\circ}=\frac{\sqrt{2}}{2}$,所以$EF = AF=AE\sin45^{\circ}=3×\frac{\sqrt{2}}{2}=\frac{3\sqrt{2}}{2}$。
已知$AC = 6$,则$CF=AC - AF=6-\frac{3\sqrt{2}}{2}$。
在$Rt\triangle CEF$中,根据勾股定理$CE^{2}=EF^{2}+CF^{2}$,$EF = AF=\frac{3\sqrt{2}}{2}$,$CF = 6-\frac{3\sqrt{2}}{2}$,则$CE^{2}=(\frac{3\sqrt{2}}{2})^{2}+(6 - \frac{3\sqrt{2}}{2})^{2}=\frac{9×2}{4}+36-2×6×\frac{3\sqrt{2}}{2}+\frac{9×2}{4}=9 + 36-18\sqrt{2}=45-18\sqrt{2}$。
因为$\triangle BCE\cong\triangle ACD$,所以$AD = BE$。
又因为$BC = AC = 6$,在$Rt\triangle BCE$中,根据勾股定理$BE^{2}=BC^{2}+CE^{2}$,$BC = 6$,$CE^{2}=45-18\sqrt{2}$,则$BE^{2}=36+(45 - 18\sqrt{2})=81-18\sqrt{2}$。
另一种方法:
因为$\triangle BCE\cong\triangle ACD$,所以$AD = BE$。
因为$\angle ACB=\angle DCE = 90^{\circ}$,$AC = BC = 6$,$\angle CAE = 45^{\circ}$,$\angle CAB = 45^{\circ}$,所以$\angle BAE=\angle BAC+\angle CAE=90^{\circ}$。
由$AC = 6$,$AE = 3$,根据勾股定理$BE=\sqrt{AB^{2}+AE^{2}}$,又因为$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{6^{2}+6^{2}}=\sqrt{72}=6\sqrt{2}$(等腰直角三角形三边关系$a:b:c = 1:1:\sqrt{2}$,这里$a = b = 6$,$c = AB$)。
所以$BE=\sqrt{(6\sqrt{2})^{2}+3^{2}}=\sqrt{72 + 9}=\sqrt{81}=9$。
所以(1)已证$\triangle BCE\cong\triangle ACD$;(2)$AD$的长为$9$。
查看更多完整答案,请扫码查看


