第28页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
1. 下列选项中的图形,不能由如图所示的图形通过平移或旋转得到的是(
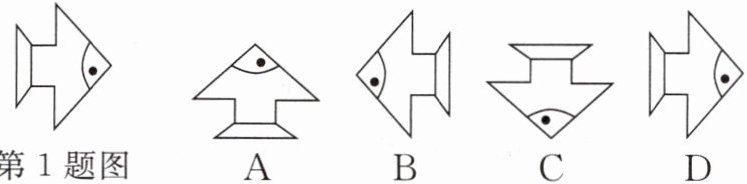
B
)
答案:
B
2. 将一个正六边形绕其中心旋转后仍与原图形重合,旋转角的大小不可能是(
A.60°
B.90°
C.180°
D.360°
B
)A.60°
B.90°
C.180°
D.360°
答案:
B
3. 如图,在△ABC中$,\angle B= 80°,\angle C= 65°,$将△ABC绕点A逆时针旋转得到△AB'C'.当AB'落在AC上时$,\angle BAC'$的度数为(
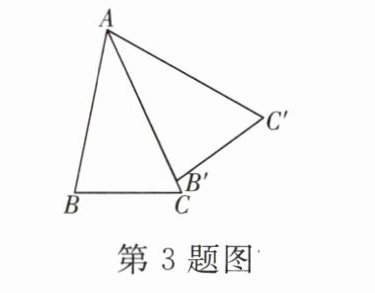
A.65°
B.70°
C.80°
D.85°
B
)
A.65°
B.70°
C.80°
D.85°
答案:
B
4. 如图,点A,B,C,D,O都在方格纸的格点(网格线的交点)上,若△COD是由△AOB绕点O顺时针旋转而得到的,则旋转的角度最小为
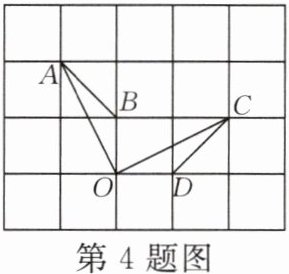
90
°.[img]
答案:
90
5. 如图,△ABC绕顶点A顺时针旋转$43°$得到△ADE.若$\angle BAE= 17°,$$\angle D= 45°,则\angle C$的度数为 ______
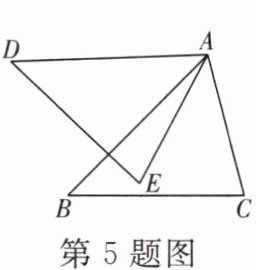
75
°.[img]
答案:
75
6. 一副三角尺如图1摆放,把三角尺AOB绕公共顶点O顺时针旋转至图2所示的位置,即AB//OD时,$\angle 1$的度数为 ______°.[img]
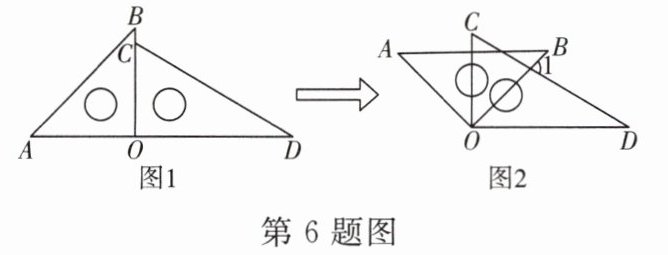

75
答案:
75
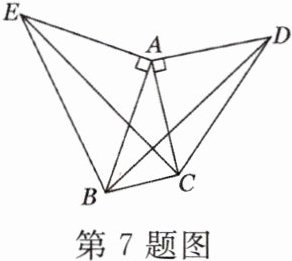
7. 如图,△ACD,△AEB都是等腰直角三角形,$\angle CAD= \angle EAB= 90^\circ,$$\angle BAC= 30^\circ,$且△EAC以某一点为旋转中心逆时针旋转后能与△BAD重合.
(1)指出旋转中心;
(2)指出旋转角度;
(3)若EC= 10 cm,求BD的长.
(1)指出旋转中心;
(2)指出旋转角度;
(3)若EC= 10 cm,求BD的长.

答案:
(1)点A
(2)90°
(3)10 cm
(1)点A
(2)90°
(3)10 cm
8. 如图,在Rt△OAB中,$\angle OAB= 90°,$OA= AB= 6,将△OAB绕点O逆时针旋转$90°$得到△OA_1B_1.
(1)线段OA_1的长为
(2)连接AA_1,求证:四边形OAA_1B_1是平行四边形;
(3)求四边形OAA_1B_1的面积.
(1)线段OA_1的长为
6
,$\angle AOB_1$的度数为135
°;(2)连接AA_1,求证:四边形OAA_1B_1是平行四边形;
证明:由旋转的性质可知:$OA = OA_{1}$,$AB = A_{1}B_{1}$,$\angle OAB=\angle OA_{1}B_{1}=90^{\circ}$,$\angle AOA_{1}=90^{\circ}$。因为$\angle OAB=\angle AOA_{1}=90^{\circ}$,所以$AB// OA_{1}$(内错角相等,两直线平行)。又因为$OA = AB = 6$,所以$OA = A_{1}B_{1}$。根据平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形,因为$AB// OA_{1}$且$AB = OA_{1}$,所以四边形$OAA_{1}B_{1}$是平行四边形。
(3)求四边形OAA_1B_1的面积.
解:因为四边形$OAA_{1}B_{1}$是平行四边形,$OA = 6$,$OA_{1}=6$,$\angle AOA_{1}=90^{\circ}$。根据平行四边形的面积公式$S =底×高$,在平行四边形$OAA_{1}B_{1}$中,以$OA$为底,$OA_{1}$为高(因为$\angle AOA_{1}=90^{\circ}$)。所以$S_{OAA_{1}B_{1}}=OA× OA_{1}=6×6 = 36$。
答案:
1. (1)
因为$\triangle OAB$绕点$O$逆时针旋转$90^{\circ}$得到$\triangle OA_{1}B_{1}$,根据旋转的性质:旋转前后对应线段长度不变,对应点与旋转中心所连线段的夹角等于旋转角。
已知$OA = 6$,所以$OA_{1}=OA = 6$。
又因为$\angle AOA_{1}=90^{\circ}$,$\angle AOB = 45^{\circ}$(在$Rt\triangle OAB$中,$\angle OAB = 90^{\circ}$,$OA = AB$,所以$\angle AOB=\angle ABO = 45^{\circ}$),则$\angle AOB_{1}=\angle AOA_{1}+\angle A_{1}OB_{1}$,而$\angle A_{1}OB_{1}=\angle AOB = 45^{\circ}$,所以$\angle AOB_{1}=90^{\circ}+45^{\circ}=135^{\circ}$。
故答案为$6$;$135$。
2. (2)
解(证明):
由旋转的性质可知:$OA = OA_{1}$,$AB = A_{1}B_{1}$,$\angle OAB=\angle OA_{1}B_{1}=90^{\circ}$,$\angle AOA_{1}=90^{\circ}$。
因为$\angle OAB=\angle AOA_{1}=90^{\circ}$,所以$AB// OA_{1}$(内错角相等,两直线平行)。
又因为$OA = AB = 6$,所以$OA = A_{1}B_{1}$。
根据平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形,因为$AB// OA_{1}$且$AB = OA_{1}$,所以四边形$OAA_{1}B_{1}$是平行四边形。
3. (3)
解:
因为四边形$OAA_{1}B_{1}$是平行四边形,$OA = 6$,$OA_{1}=6$,$\angle AOA_{1}=90^{\circ}$。
根据平行四边形的面积公式$S =底×高$,在平行四边形$OAA_{1}B_{1}$中,以$OA$为底,$OA_{1}$为高(因为$\angle AOA_{1}=90^{\circ}$)。
所以$S_{OAA_{1}B_{1}}=OA× OA_{1}$(根据平行四边形面积公式$S = a× h$,这里$a = OA$,$h = OA_{1}$)。
已知$OA = OA_{1}=6$,则$S_{OAA_{1}B_{1}}=6×6 = 36$。
综上,(1)$6$,$135$;(2)证明过程如上述;(3)$36$。
因为$\triangle OAB$绕点$O$逆时针旋转$90^{\circ}$得到$\triangle OA_{1}B_{1}$,根据旋转的性质:旋转前后对应线段长度不变,对应点与旋转中心所连线段的夹角等于旋转角。
已知$OA = 6$,所以$OA_{1}=OA = 6$。
又因为$\angle AOA_{1}=90^{\circ}$,$\angle AOB = 45^{\circ}$(在$Rt\triangle OAB$中,$\angle OAB = 90^{\circ}$,$OA = AB$,所以$\angle AOB=\angle ABO = 45^{\circ}$),则$\angle AOB_{1}=\angle AOA_{1}+\angle A_{1}OB_{1}$,而$\angle A_{1}OB_{1}=\angle AOB = 45^{\circ}$,所以$\angle AOB_{1}=90^{\circ}+45^{\circ}=135^{\circ}$。
故答案为$6$;$135$。
2. (2)
解(证明):
由旋转的性质可知:$OA = OA_{1}$,$AB = A_{1}B_{1}$,$\angle OAB=\angle OA_{1}B_{1}=90^{\circ}$,$\angle AOA_{1}=90^{\circ}$。
因为$\angle OAB=\angle AOA_{1}=90^{\circ}$,所以$AB// OA_{1}$(内错角相等,两直线平行)。
又因为$OA = AB = 6$,所以$OA = A_{1}B_{1}$。
根据平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形,因为$AB// OA_{1}$且$AB = OA_{1}$,所以四边形$OAA_{1}B_{1}$是平行四边形。
3. (3)
解:
因为四边形$OAA_{1}B_{1}$是平行四边形,$OA = 6$,$OA_{1}=6$,$\angle AOA_{1}=90^{\circ}$。
根据平行四边形的面积公式$S =底×高$,在平行四边形$OAA_{1}B_{1}$中,以$OA$为底,$OA_{1}$为高(因为$\angle AOA_{1}=90^{\circ}$)。
所以$S_{OAA_{1}B_{1}}=OA× OA_{1}$(根据平行四边形面积公式$S = a× h$,这里$a = OA$,$h = OA_{1}$)。
已知$OA = OA_{1}=6$,则$S_{OAA_{1}B_{1}}=6×6 = 36$。
综上,(1)$6$,$135$;(2)证明过程如上述;(3)$36$。
查看更多完整答案,请扫码查看


