第39页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
1. 如图,将$\odot O沿着弦AB$翻折,劣弧恰好经过圆心$O$.如果弦$AB= 4\sqrt{3}$,那么$\odot O$的半径为(
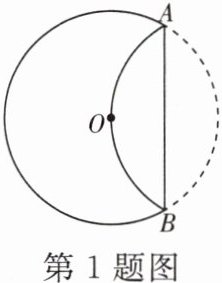
A.2
B.4
C.$2\sqrt{3}$
D.$4\sqrt{3}$
B
)
A.2
B.4
C.$2\sqrt{3}$
D.$4\sqrt{3}$
答案:
B
2. 如图,在半径为5的$\odot O$中,$AB$,$CD$是互相垂直的两条弦,垂足为$P$.若$AB= CD= 8$,则$OP$的长为(
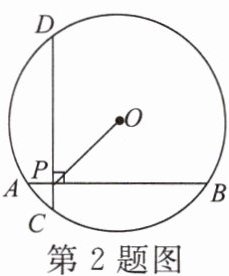
A.3
B.4
C.$3\sqrt{2}$
D.$4\sqrt{2}$
C
)
A.3
B.4
C.$3\sqrt{2}$
D.$4\sqrt{2}$
答案:
C
3. 如图,在$\odot O$中,若弦$AB= 1$,点$C在AB$上移动,连接$OC$,过点$C作CD\perp OC交\odot O于点D$,则$CD$长的最大值为
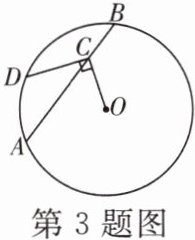
$\frac{1}{2}$
.
答案:
$\frac{1}{2}$
4. 如图,射线$PB$,$PD分别交\odot O于点A$,$B和点C$,$D$,且$AB= CD= 8$.若$\odot O$的半径为5,$OA// PC$,则$OP$的长为______.
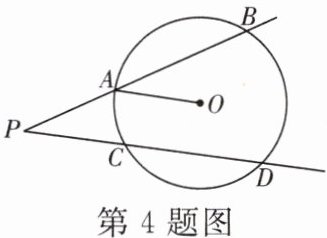

$3\sqrt{10}$
答案:
$3\sqrt{10}$
5. 如图,某窗户由矩形和弓形组成,已知弓形的跨度$AB= 4$ m,弓形的高$EF= 1$ m.现计划安装玻璃,求出$\overset{\frown}{AB}所在\odot O$的半径.
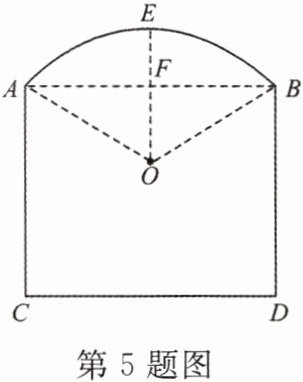

答案:
2.5 m
6. 如图所示为一个隧道的横截面,它的形状是以点$O$为圆心的圆的一部分.如果$M是\odot O中弦CD$的中点,$EM经过圆心O交\odot O于点E$,$CD= 10$,$EM= 25$.求$\odot O$的半径.


答案:
13
7. 筒车是一种以水流作动力,取水灌田的工具,据史料记载,它发明于隋而盛于唐,距今已有1000多年的历史,是我国古代劳动人民的一项伟大创造.
如图,筒车盛水筒的运行轨迹是以轴心$O$为圆心的圆,已知圆心$O$在水面上方,且当圆被水面截得的弦$AB$为6 m时,水面下盛水筒的最大深度为1 m(即水面下方圆上一点距离水面的最大距离).
(1)求该圆的半径;
(2)若水面上涨导致圆被水面截得的弦$AB$从原来的6 m变为8 m时,则水面上涨的高度为多少米?
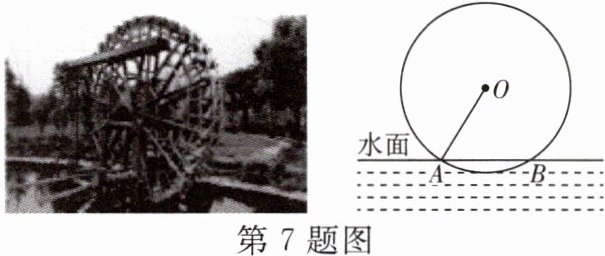
如图,筒车盛水筒的运行轨迹是以轴心$O$为圆心的圆,已知圆心$O$在水面上方,且当圆被水面截得的弦$AB$为6 m时,水面下盛水筒的最大深度为1 m(即水面下方圆上一点距离水面的最大距离).
(1)求该圆的半径;
(2)若水面上涨导致圆被水面截得的弦$AB$从原来的6 m变为8 m时,则水面上涨的高度为多少米?

答案:
(1)5 m
(2)1 m
(1)5 m
(2)1 m
查看更多完整答案,请扫码查看


