《2025年全效学习课时提优九年级数学全一册人教版精华版》

11. 我国古代数学名著《九章算术》中有一题：“今有圆材,径二尺五寸.欲为方版,令厚七寸,问广几何？”结合下图,其大意是：今有圆形木材,直径 BD 为 25 寸,要做成方形板材,使其厚度 CD 达到 7 寸,则 BC 的长为(C)

A.$\sqrt{674}$寸
B.25 寸
C.24 寸
D.7 寸

答案： C

12. 如图,在$\odot O$中,AB 是$\odot O$的直径,$AB= \sqrt{2}AC$,$\angle ODC= 12^{\circ}$,则$\angle DBC$的度数为(B)

A.$80^{\circ}$
B.$102^{\circ}$
C.$120^{\circ}$
D.$135^{\circ}$

答案： B

13. 如图,四边形 ABCD 内接于$\odot O$,$BC// AD$,$AC\perp BD$.若$\angle AOD= 120^{\circ}$,$AD= \sqrt{3}$,则$\angle CAO$的度数与 BC 的长分别为(C)

 A.$10^{\circ}$,1

B.$10^{\circ}$,$\sqrt{2}$
C.$15^{\circ}$,1
D.$15^{\circ}$,$\sqrt{2}$

答案： C

14. 如图,点 A,B,C,D 在半径为 2 的$\odot O$上,$\angle ACB= 60^{\circ}$,$OD\perp AB$,垂足为 E,连接 OA,则 OE 的长度为1.

答案： 1

15. 如图,四边形 ABCD 内接于$\odot O$,AC 为$\odot O$的直径,$\angle ADB= \angle CDB$.
(1)试判断$\triangle ABC$的形状,并给出证明；
(2)若$AB= 5\sqrt{2}$,$AD= 6$,求 CD 的长.

答案： 1. （1）
证明$\triangle ABC$的形状：
因为$AC$为$\odot O$的直径，所以$\angle ABC = 90^{\circ}$（直径所对的圆周角是直角）。
又因为$\angle ADB=\angle CDB$，$\angle ADB=\angle ACB$（同弧所对的圆周角相等，弧$AB$所对的圆周角$\angle ADB$和$\angle ACB$），$\angle CDB=\angle CAB$（同弧所对的圆周角相等，弧$BC$所对的圆周角$\angle CDB$和$\angle CAB$）。
所以$\angle ACB=\angle CAB$。
在$\triangle ABC$中，根据等角对等边，$AB = BC$。
因为$\angle ABC = 90^{\circ}$且$AB = BC$，所以$\triangle ABC$是等腰直角三角形。
2. （2）
解：
因为$\triangle ABC$是等腰直角三角形，$AB = 5\sqrt{2}$，由勾股定理$AC^{2}=AB^{2}+BC^{2}$，且$AB = BC$，则$AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{2AB^{2}}$。
把$AB = 5\sqrt{2}$代入得$AC=\sqrt{2×(5\sqrt{2})^{2}}=\sqrt{2×50}=10$。
因为$AC$为直径，所以$\angle ADC = 90^{\circ}$（直径所对的圆周角是直角）。
在$Rt\triangle ADC$中，根据勾股定理$CD=\sqrt{AC^{2}-AD^{2}}$。
已知$AD = 6$，$AC = 10$，则$CD=\sqrt{10^{2}-6^{2}}=\sqrt{100 - 36}=\sqrt{64}=8$。
综上，（1）$\triangle ABC$是等腰直角三角形；（2）$CD$的长为$8$。

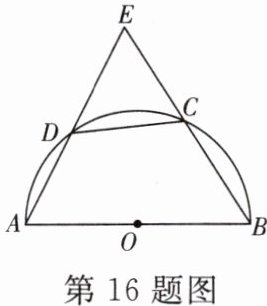
16. 如图,四边形 ABCD 内接于$\odot O$,AB 是直径,C 是$\widehat{BD}$的中点,延长 AD 交 BC 的延长线于点 E.求证:$CE= CD$.

答案： 证明：
∵四边形ABCD内接于⊙O，
∴∠CDE=∠ABC（圆内接四边形的外角等于内对角）。
∵C是$\widehat{BD}$的中点，
∴$\widehat{CD}=\widehat{CB}$，
∴∠CAD=∠CAB（等弧所对的圆周角相等）。
∵AB是⊙O的直径，
∴∠ACB=90°（直径所对的圆周角是直角），
∴∠ACE=∠ACB=90°。
在△AEC和△ABC中，
$\left\{\begin{array}{l}∠CAE=∠CAB\\AC=AC\\∠ACE=∠ACB\end{array}\right.$，
∴△AEC≌△ABC（ASA），
∴∠E=∠ABC。
又
∵∠CDE=∠ABC，
∴∠E=∠CDE，
∴CE=CD。

17.[推理能力]如图,圆内接四边形 ABCD 的对角线 AC,BD 相交于点 E,BD 平分$\angle ABC$,$\angle BAC= \angle ADB$.
(1)求证:DB 平分$\angle ADC$,并求$\angle BAD$的大小；
(2)过点 C 作$CF// AD$交 AB 的延长线于点 F,若$AC= AD$,$BF= 2$,求此圆的半径.

答案： 1. （1）
证明$DB$平分$\angle ADC$：
因为$\angle BAC$与$\angle BDC$是同弧所对的圆周角，所以$\angle BAC = \angle BDC$。
又因为$\angle BAC=\angle ADB$，所以$\angle ADB=\angle BDC$，即$DB$平分$\angle ADC$。
求$\angle BAD$的大小：
因为$BD$平分$\angle ABC$，所以$\angle ABD=\angle CBD$。
又因为$\angle BAC = \angle BDC$，$\angle ADB=\angle BDC$，$\angle ABD+\angle BAD+\angle ADB = 180^{\circ}$，$\angle CBD+\angle BCD+\angle BDC = 180^{\circ}$。
设$\angle ABD=\angle CBD = x$，$\angle ADB=\angle BDC = y$。
因为$\angle BAC = y$，在$\triangle ABC$中，$\angle BAC+\angle ABC+\angle ACB = 180^{\circ}$，且$\angle ACB=\angle ADB = y$（同弧所对的圆周角相等）。
所以$y + 2x+y=180^{\circ}$，又因为$\angle BAD=\angle BAC+\angle CAD$，$\angle CAD=\angle CBD=x$（同弧所对的圆周角相等），$\angle BAC = y$，$\angle ABD=x$，$\angle ADB = y$，$\angle ABD+\angle BAD+\angle ADB = 180^{\circ}$，即$x+(y + x)+y=180^{\circ}$，化简得$2(x + y)=180^{\circ}$，所以$x + y = 90^{\circ}$，则$\angle BAD=90^{\circ}$。
2. （2）
因为$CF// AD$，所以$\angle F=\angle BAD = 90^{\circ}$，$\angle FCB=\angle ADB$。
又因为$\angle ADB=\angle BDC=\angle BAC$，$\angle BAC=\angle BDC$，$\angle FCB=\angle BDC$，$\angle FBC=\angle CAD$（圆内接四边形外角等于内对角）。
因为$AC = AD$，所以$\angle ACD=\angle ADC$，$\angle BAC=\angle ADB$，$\angle ADB=\angle BDC$，$\angle BAC=\angle BDC$，$\angle CAD=\angle CBD$，$\angle ABD=\angle CBD$。
可证$\triangle ABC\cong\triangle FBC(AAS)$（$\angle BAC=\angle BFC = 90^{\circ}$，$\angle ABC=\angle FBC$，$BC = BC$）。
所以$AB=BF = 2$。
因为$\angle BAD = 90^{\circ}$，所以$BD$是圆的直径（$90^{\circ}$的圆周角所对的弦是直径）。
又因为$AC = AD$，$\angle BAD = 90^{\circ}$，所以$\triangle ABD$是等腰直角三角形（$\angle ABD=\angle ADB = 45^{\circ}$）。
根据勾股定理$BD=\sqrt{AB^{2}+AD^{2}}$，因为$AB = 2$，$AD = AB = 2$（等腰直角三角形两直角边相等），所以$BD=\sqrt{2^{2}+2^{2}}=\sqrt{8}=2\sqrt{2}$。
所以圆的半径$R=\frac{BD}{2}=\sqrt{2}$。
综上，（1）$DB$平分$\angle ADC$，$\angle BAD = 90^{\circ}$；（2）圆的半径为$\sqrt{2}$。