《2025年全效学习课时提优九年级数学全一册人教版精华版》

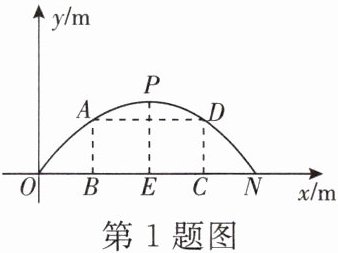
1. 某校想将新建图书楼的正门设计为一个抛物线形拱门,设计方案如图所示. 抛物线形拱门的跨度ON= 12 m,拱高PE= 4 m. 其中,点N在x轴上,PE⊥ON,OE= EN. 现要求在拱门中设置矩形框架ABCD,点A,D在抛物线上,边BC在ON上.
(1)求抛物线的函数解析式；
(2)当AB= 3 m时,求矩形框架ABCD的面积.

答案：
(1)$y=-\frac{1}{9}x^{2}+\frac{4}{3}x$
(2)$18\ m^{2}$

2. 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图所示,甲在点O正上方1 m的P处发出一球,羽毛球飞行的高度y(单位:m)与水平距离x(单位:m)之间满足函数解析式$y= a(x-4)^2+h. $已知点O与球网的水平距离为5 m,球网的高度为1.55 m.
(1)当a= -1/24时,
①求h的值；
②通过计算判断此球能否过网；
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7 m,离地面的高度为12/5 m的点Q处时,乙扣球成功,求a的值.

答案：
(1)①$h=\frac{5}{3}$ ②能
(2)$a=-\frac{1}{5}$

3. 如图1是一座抛物线形拱桥$C_1$的示意图. 水面宽AB与桥面长CD均为24 m,点E在CD上,DE= 6 m,测得点E到正下方桥拱的距离EF为1.5 m,以桥拱顶点O为原点,桥面为x轴建立平面直角坐标系.

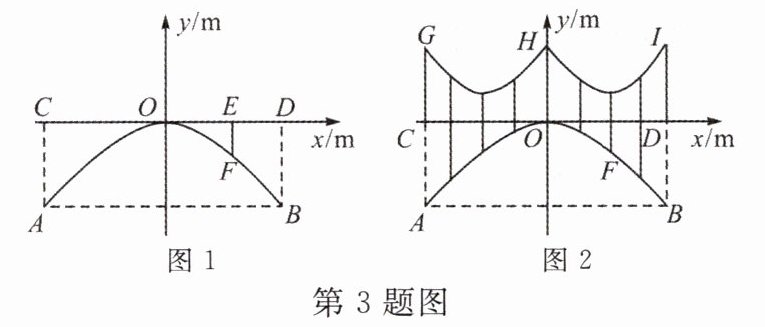
(1)求桥拱顶部O离水面的距离；
(2)如图2,在(1)的条件下,桥面上方有3根高度均为4 m的支柱CG,OH,DI,过相邻两根支柱顶端的钢缆是形状相同的抛物线$C_2,C_3(C_2$在$C_3$右侧),其最低点与桥面CD的距离均为1 m. 求拱桥抛物线$C_1$与钢缆抛物线$C_2$的竖直距离的最小值.

答案：
(1)6 m
(2)2 m