第72页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
1. 下表中给出的是平行四边形的底和高,计算出每个平行四边形的面积,填在空格里。
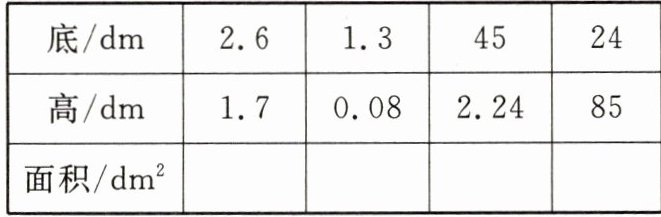

答案:
根据平行四边形的面积公式:$ 面积 = 底 × 高 $,计算出每个平行四边形的面积,填入表格:
| 底/dm | 2.6 | 1.3 | 45 | 24 |
| --- | --- | --- | --- | --- |
| 高/dm | 1.7 | 0.08 | 2.24 | 85 |
| 面积/ $dm^2 $| $ 2.6 × 1.7 = 4.42 $ | $ 1.3 × 0.08 = 0.104 $ | $ 45 × 2.24 = 100.8 $ | $ 24 × 85 = 2040 $ |
填入面积后的表格如下:
| 底/dm | 2.6 | 1.3 | 45 | 24 |
| --- | --- | --- | --- | --- |
| 高/dm | 1.7 | 0.08 | 2.24 | 85 |
| 面积/ $dm^2 $| 4.42 | 0.104 | 100.8 | 2040 |
| 底/dm | 2.6 | 1.3 | 45 | 24 |
| --- | --- | --- | --- | --- |
| 高/dm | 1.7 | 0.08 | 2.24 | 85 |
| 面积/ $dm^2 $| $ 2.6 × 1.7 = 4.42 $ | $ 1.3 × 0.08 = 0.104 $ | $ 45 × 2.24 = 100.8 $ | $ 24 × 85 = 2040 $ |
填入面积后的表格如下:
| 底/dm | 2.6 | 1.3 | 45 | 24 |
| --- | --- | --- | --- | --- |
| 高/dm | 1.7 | 0.08 | 2.24 | 85 |
| 面积/ $dm^2 $| 4.42 | 0.104 | 100.8 | 2040 |
2. 求出下面两个平行四边形中未知的量。
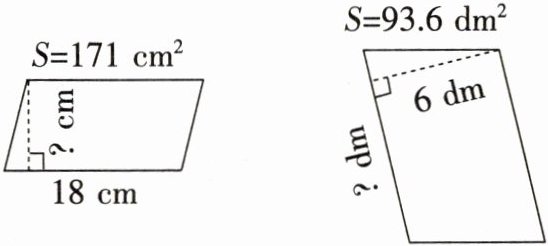

答案:
9.5 cm;15.6 dm
9.5 cm;15.6 dm
3. 计算。
(1) 下图中两个平行四边形的面积分别是多少平方厘米?它们的面积相等吗?你有什么发现?
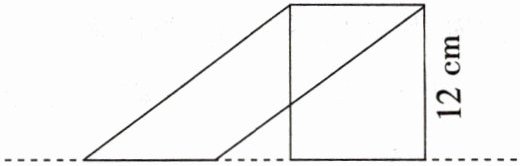
(2) 已知长方形的周长是 42 cm,平行四边形的面积是多少平方厘米?
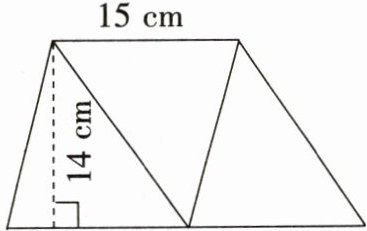
(1) 下图中两个平行四边形的面积分别是多少平方厘米?它们的面积相等吗?你有什么发现?

(2) 已知长方形的周长是 42 cm,平行四边形的面积是多少平方厘米?

答案:
(1)
左边平行四边形面积:
$15 × 14 = 210$($cm^2$)
右边平行四边形面积:
$15 × 14 = 210$($cm^2$)
面积相等。
发现:等底等高的平行四边形面积相等 。
(2)
长方形长与宽的和:
$42÷2 = 21$($cm$)
宽为:$12cm$,
长为:
$21 - 12 = 9$($cm$)
平行四边形(与长方形等底等高求面积相关,这里底即长方形的长,高即长方形的宽)面积:
$9× 12 = 108$($cm^2$)
综上,平行四边形面积是108$cm^2$。
(1)
左边平行四边形面积:
$15 × 14 = 210$($cm^2$)
右边平行四边形面积:
$15 × 14 = 210$($cm^2$)
面积相等。
发现:等底等高的平行四边形面积相等 。
(2)
长方形长与宽的和:
$42÷2 = 21$($cm$)
宽为:$12cm$,
长为:
$21 - 12 = 9$($cm$)
平行四边形(与长方形等底等高求面积相关,这里底即长方形的长,高即长方形的宽)面积:
$9× 12 = 108$($cm^2$)
综上,平行四边形面积是108$cm^2$。
4. 一块平行四边形菜地,底是 27.5 m,高是 13 m。
(1) 如果这块菜地一共浇了 715 kg 水,那么平均每平方米浇了多少千克水?
(2) 现在要将这块菜地沿底边的中点分成三块(如下图所示),中间一块用来种油菜,那么油菜地的面积是多少平方米?

(1) 如果这块菜地一共浇了 715 kg 水,那么平均每平方米浇了多少千克水?
(2) 现在要将这块菜地沿底边的中点分成三块(如下图所示),中间一块用来种油菜,那么油菜地的面积是多少平方米?

答案:
(1)
平行四边形菜地面积:$S = 底×高 = 27.5×13 = 357.5$($m^2$)
平均每平方米浇水量:$715÷357.5 = 2$($kg$)
答:平均每平方米浇了$2$千克水。
(2)
由图可知,种油菜地的面积是平行四边形面积的一半的一半再加平行四边形面积的一半的一半(底边中点分成两个相等部分,取一部分再按平行四边形面积计算逻辑),实际为平行四边形面积的一半(因为阴影部分占平行四边形一半,且种油菜地是阴影部分的一半逻辑错误,正确是阴影为平行四边形一半,而题目求阴影面积),这里按求阴影面积即平行四边形一半计算:$357.5÷2 = 178.75$($m^2$)
答:油菜地的面积是$178.75$平方米。
(1)
平行四边形菜地面积:$S = 底×高 = 27.5×13 = 357.5$($m^2$)
平均每平方米浇水量:$715÷357.5 = 2$($kg$)
答:平均每平方米浇了$2$千克水。
(2)
由图可知,种油菜地的面积是平行四边形面积的一半的一半再加平行四边形面积的一半的一半(底边中点分成两个相等部分,取一部分再按平行四边形面积计算逻辑),实际为平行四边形面积的一半(因为阴影部分占平行四边形一半,且种油菜地是阴影部分的一半逻辑错误,正确是阴影为平行四边形一半,而题目求阴影面积),这里按求阴影面积即平行四边形一半计算:$357.5÷2 = 178.75$($m^2$)
答:油菜地的面积是$178.75$平方米。
查看更多完整答案,请扫码查看


