《2025年作业本江西教育出版社五年级数学上册人教版》

1. 想一想，填一填。
(1) 等式的性质：①等式两边（ ），左右两边仍然相等；②等式两边（ ），左右两边仍然相等。

答案： ①加上或减去同一个数；②乘同一个数，或除以同一个不为0的数

(2) 看图填空。

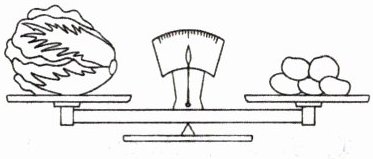
1 棵白菜和（ ）个马铃薯同样重。左边再放上（ ）棵白菜，右边再放上（ ）个土豆，天平还保持平衡。

答案： 5  1  5

(3) 已知 $ x = y $，请根据等式的性质填空。
$ x + 2.05 = y + (\ ) $
$ x × 100 = y × (\ ) $
$ x - (\ ) = y - a $
$ x ÷ (\ ) = y ÷ m $（$ m $不为 0）

答案：
(3) 2.05；100；a；m

(4) 已知 $ 2(m - 5) = 4n $，等式两边同时（ ），原式可以变形为 $ m - 5 = 2n $；等式两边同时（ ），原式可以变形为 $ 2m = 4n + 10 $。

答案：
(4) 除以2；加10

2. 根据等式的性质，对下列方程进行变形，在（ ）里填上运算符号或合适的数。
(1) $ x - 12.9 = 45 $
$ x - 12.9 + 12.9 = 45(\ )(\ ) $
(2) $ 13.8 = 45 - x $
$ 13.8(\ )(\ ) = 45 - x + x $
(3) $ 39x = 78 $
$ 39x ÷ 39 = 78(\ )(\ ) $
(4) $ x ÷ 39 = 78 $
$ x ÷ 39(\ )(\ ) = 78 × 39 $
(5) $ 39 ÷ x = 78 $
$ 39 ÷ x × (\ ) = 78 × x $
(6) $ (x - 39) ÷ 3 = 78 $
$ (x - 39) ÷ 3 × 3 = 78(\ )(\ ) $

答案：
(1) $x - 12.9 = 45$
$x - 12.9 + 12.9 = 45( + )(12.9)$
(2) $13.8 = 45 - x$
$13.8( + )(x) = 45 - x + x$
(3) $39x = 78$
$39x ÷ 39 = 78( ÷ )(39)$
(4) $x ÷ 39 = 78$
$x ÷ 39( × )(39) = 78 × 39$
(5) $39 ÷ x = 78$
$39 ÷ x × (x) = 78 × x$
(6) $(x - 39) ÷ 3 = 78$
$(x - 39) ÷ 3 × 3 = 78( × )(3)$

3. 已知 $ ▲ + ● + ■ = 23 $，$ ▲ + ▲ + ● = 28 $，$ ▲ + ▲ + ● + ● = 32 $，那么 $ ▲ = (\ ) $，$ ■ = (\ ) $，$ ● = (\ ) $。

答案： 设▲为$a$，●为$b$，■为$c$。
根据题意得：
$\begin{cases}a + b + c = 23, \\ 2a + b = 28, \\2a + 2b = 32.\end{cases}$
由$2a + 2b = 32$可得：
$a + b = 16$，
将$a + b = 16$代入$a + b + c = 23$可得：
$16 + c = 23$，
解得：
$c = 7$，
将$a + b = 16$代入$2a + b = 28$可得：
$2a+b-(a + b)=28-16$，
即：
$a = 12$，
将$a = 12$代入$a + b = 16$可得：
$12 + b = 16$，
解得：
$b = 4$，
因此，$\begin{cases}▲ = 12, \\■ = 7, \\● = 4.\end{cases}$

4. 现在有一架天平和两个砝码，一个砝码是 $ 5g $，一个砝码是 $ 2g $，怎么用天平称出 $ 3g $的食盐？

答案： 1. 将5g砝码放在天平右盘，2g砝码放在天平左盘。
2. 向左盘添加食盐，直至天平平衡。
3. 左盘食盐的质量即为3g。