第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
1. 盒子里有三种不同颜色的小球,每个小球的大小相同。晨晨每次摸出一个小球,记录下它的颜色,再放回去摇匀,重复了 60 次,摸出小球的情况如下表所示。
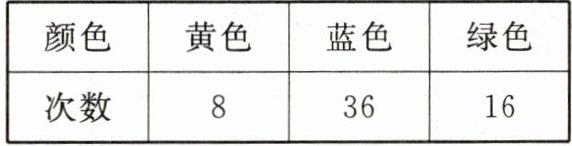
(1) 根据表中的数据推测,盒子里()色小球的数量可能最多,()色小球的数量可能最少。
(2) 如果再摸 1 次,最有可能摸到()色小球。

(1) 根据表中的数据推测,盒子里()色小球的数量可能最多,()色小球的数量可能最少。
(2) 如果再摸 1 次,最有可能摸到()色小球。
答案:
(1)蓝;黄
(2)蓝
(1)蓝;黄
(2)蓝
(1)下表记录的是小明从袋子中摸 30 次球得到的结果,他最有可能是在装有()的袋子里摸的。(每次摸出一个球后再放回去)
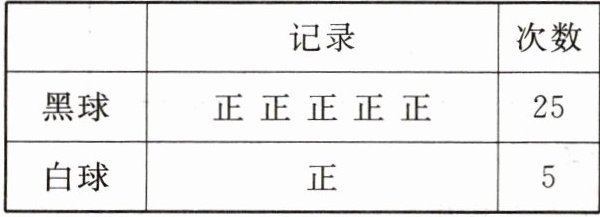
A.5 个黑球
B.4 个黑球和 1 个白球
C.5 个白球
D.1 个黑球和 4 个白球

A.5 个黑球
B.4 个黑球和 1 个白球
C.5 个白球
D.1 个黑球和 4 个白球
答案:
B
3. 某书店举办一个抽奖活动,每位书店会员都可以转动转盘抽奖一次,指针停在哪个位置,就可以兑换相应的奖品。
如果你是这家书店的老板,你会把以上四种奖项分别填在转盘的什么位置上?
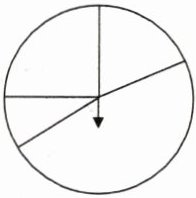
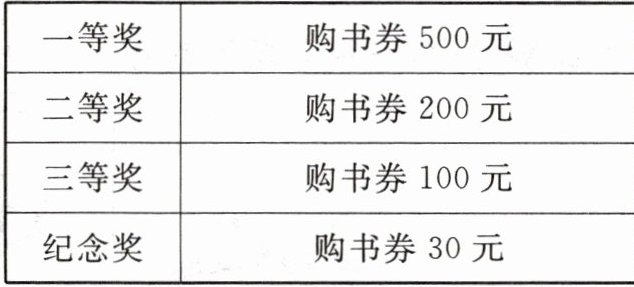
如果你是这家书店的老板,你会把以上四种奖项分别填在转盘的什么位置上?


答案:
最大区域填纪念奖,第二大区域填三等奖,第三大区域填二等奖,最小区域填一等奖。
4. 掷一掷,填一填。
跳跳和涛涛同时各掷 1 个骰子,得到两个点数,它们的积可能是多少?
(1)完成下面的表格。

(2)如果两个点数的积大于 20 算跳跳赢,否则算涛涛赢,这个比赛公平吗?为什么?
跳跳和涛涛同时各掷 1 个骰子,得到两个点数,它们的积可能是多少?
(1)完成下面的表格。

(2)如果两个点数的积大于 20 算跳跳赢,否则算涛涛赢,这个比赛公平吗?为什么?
答案:
(1)
|积|1|2|3|4|5|6|
|----|----|----|----|----|----|----|
|1|1|2|3|4|5|6|
|2|2|4|6|8|10|12|
|3|3|6|9|12|15|18|
|4|4|8|12|16|20|24|
|5|5|10|15|20|25|30|
|6|6|12|18|24|30|36|
(2)
不公平。
两个骰子点数之积大于20的情况有:$5×5 = 25$,$5×6 = 30$,$6×5 = 30$,$6×6 = 36$,$4×6 = 24$,$6×4 = 24$,共6种。
两个骰子点数之积小于等于20的情况有:$36 - 6=30$种。
因为跳跳赢的可能性小于涛涛赢的可能性,所以这个比赛不公平。
(1)
|积|1|2|3|4|5|6|
|----|----|----|----|----|----|----|
|1|1|2|3|4|5|6|
|2|2|4|6|8|10|12|
|3|3|6|9|12|15|18|
|4|4|8|12|16|20|24|
|5|5|10|15|20|25|30|
|6|6|12|18|24|30|36|
(2)
不公平。
两个骰子点数之积大于20的情况有:$5×5 = 25$,$5×6 = 30$,$6×5 = 30$,$6×6 = 36$,$4×6 = 24$,$6×4 = 24$,共6种。
两个骰子点数之积小于等于20的情况有:$36 - 6=30$种。
因为跳跳赢的可能性小于涛涛赢的可能性,所以这个比赛不公平。
查看更多完整答案,请扫码查看


