《2025年作业本江西教育出版社五年级数学上册人教版》

1. 除数是小数的除法计算:先移动除数的小数点,使它变成;除数的小数点向右移动几位,的小数点也向右移动几位(位数不够的,在的末尾用补足);然后按除数是的小数除法进行计算。

答案： 整数；被除数；被除数；0；整数

2. 列竖式计算。
$3.6÷0.15=$
$19.5÷0.13=$

答案： 24   150

3. 先算一算,再说说你发现了什么。

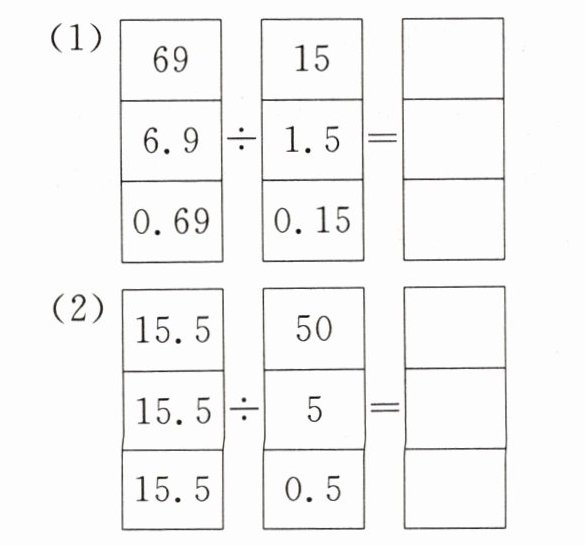
我发现:①被除数和除数同时除以相同的数(0 除外),商;②被除数不变,除数越小,商越。

答案：
(1)
69 ÷ 15 = 4.6
6.9 ÷ 1.5 = 4.6
0.69 ÷ 0.15 = 4.6
(2)
15.5 ÷ 50 = 0.31
15.5 ÷ 5 = 3.1
15.5 ÷ 0.5 = 31
我发现:
① 被除数和除数同时除以相同的数(0 除外),商不变;
② 被除数不变,除数越小,商越大。

4. 在$◯$里填上“＞”“＜”或“=”。
$5.37÷0.25◯5.37$
$4.96÷1◯4.96$
$2.14÷0.3◯2.14$
$0.99÷8.9◯0.99$

答案： 5.37÷0.25＞5.37
4.96÷1=4.96
2.14÷0.3＞2.14
0.99÷8.9＜0.99

5. 将一条 2.7 m 长的纸带按每 7.5 cm 裁成一段做成圆环,一共可以做成多少个圆环?

答案： 首先，将纸带的总长度从米转换为厘米，因为1米等于100厘米，所以：
$2.7m = 270cm$；
接下来，用纸带的总长度除以每段圆环的长度来计算可以制成的圆环数量：
$270cm {÷} 7.5cm/段 = 36$（段）；
由于不能制作不完整的圆环，所以取整数部分，即可以做成36个完整的圆环。
答：一共可以做成36个圆环。

6. 王奶奶买了一些花生榨花生油。如果5.4 kg 花生能榨出 2.16 kg 花生油,那么要榨出 1 kg 花生油需要多少千克花生?

答案： 5.4÷2.16=2.5(kg)
答：要榨出1kg花生油需要2.5千克花生。