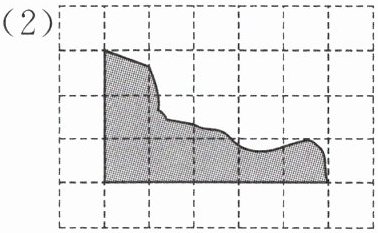
1. 图中每个小正方形的面积是$ 1 cm^2,$请你估计这个阴影图形的面积。
(1)这个图形中满格的有
(2)还可以把这个图形转化为近似的
(1)这个图形中满格的有
6
格,不满格的有12
格,这个图形的面积在6
$cm^2~$18
$cm^2 $之间。如果不满一格按半格计算,那么,这个图形的面积是12
$cm^2。$ (2)还可以把这个图形转化为近似的
梯形
,可以这样计算:(上底+下底)×高÷2=(3+6)×2÷2=9cm²
。
答案:
(1)6;12;6;18;12
(2)梯形;(上底+下底)×高÷2=(3+6)×2÷2=9cm²
(1)6;12;6;18;12
(2)梯形;(上底+下底)×高÷2=(3+6)×2÷2=9cm²
2. 选择。
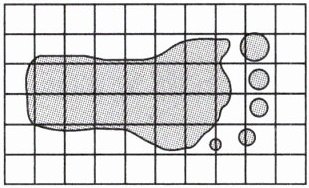
(1)小敏出生时的脚印的面积大约是(
A. 32
B. 21
C. 15
D. 12
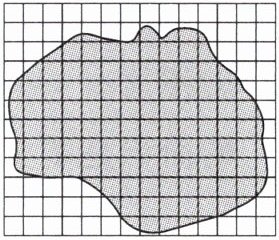
(2)右图是李伯伯家的一块空地,李伯伯想在这块空地上种植果树,每棵果树占地 3 平方米,250 棵果树(
A. 能
B. 不能
C. 无法确定
(1)小敏出生时的脚印的面积大约是(
B
$)cm^2。$(每个小正方形的面积是$ 1 cm^2) $A. 32
B. 21
C. 15
D. 12

(2)右图是李伯伯家的一块空地,李伯伯想在这块空地上种植果树,每棵果树占地 3 平方米,250 棵果树(
A
)种下。(每个小正方形的面积是 10 平方米) A. 能
B. 不能
C. 无法确定

答案:
(1)通过数方格的方法,脚印大约占了$21$个小正方形。
因为每个小正方形面积是$1cm^2$,所以脚印面积大约是$21cm^2$。
答案为B。
(2)空地中大约有$90$个小正方形,每个小正方形面积是$10$平方米。
则空地面积大约为$90×10 = 900$(平方米)。
每棵果树占地$3$平方米,$250$棵果树占地面积为$250×3 = 750$(平方米)。
因为$900>750$,所以$250$棵果树能种下。
答案为A。
因为每个小正方形面积是$1cm^2$,所以脚印面积大约是$21cm^2$。
答案为B。
(2)空地中大约有$90$个小正方形,每个小正方形面积是$10$平方米。
则空地面积大约为$90×10 = 900$(平方米)。
每棵果树占地$3$平方米,$250$棵果树占地面积为$250×3 = 750$(平方米)。
因为$900>750$,所以$250$棵果树能种下。
答案为A。
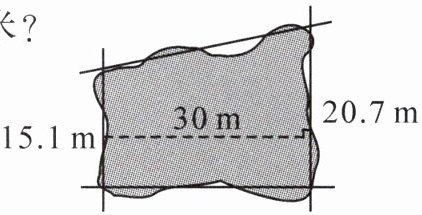
3. 有一块草坪如右图所示,这块草坪的面积大约是多少平方米?

答案:
(15.1+20.7)×30÷2=537(平方米)
答:这块草坪的面积大约是537平方米。
答:这块草坪的面积大约是537平方米。
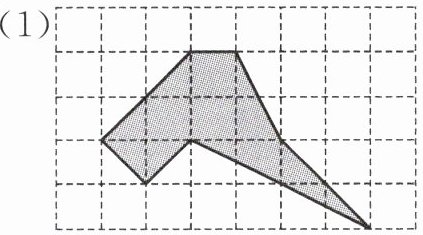
4. 图中每个小正方形的边长都是 2 dm,求阴影部分的面积。
(1)
(2)
(1)

(2)

答案:
(1)
解析:本题考查组合图形的面积计算,可通过分割法将阴影部分分割成梯形和三角形,分别计算它们的面积,再将结果相加。
梯形的上底为$2× 4 = 8$($\text{dm}$),下底为$2× 2 = 4$($\text{dm}$),高为$2× 2 = 4$($\text{dm}$);三角形的底为$2× 2 = 4$($\text{dm}$),高为$2× 2 = 4$($\text{dm}$)。
根据梯形面积公式$S_1=(a + b)h÷2$(其中$a$为上底,$b$为下底,$h$为高),可得梯形面积为$(8 + 4)×4÷2 = 24$($\text{dm}^2$)。
根据三角形面积公式$S_2 = ah÷2$(其中$a$为底,$h$为高),可得三角形面积为$4×4÷2 = 8$($\text{dm}^2$)。
则阴影部分面积$S = S_1+S_2 = 24 + 8=32$($\text{dm}^2$)。
答案:$32\text{dm}^2$。
(2)
解析:本题考查不规则图形面积的计算,可采用添补法,用大长方形的面积减去空白部分的面积。
大长方形的长为$2× 6 = 12$($\text{dm}$),宽为$2× 4 = 8$($\text{dm}$);空白部分可看作一个梯形和一个三角形,梯形上底为$2× 2 = 4$($\text{dm}$),下底为$2× 4 = 8$($\text{dm}$),高为$2× 2 = 4$($\text{dm}$);三角形底为$2× 6 = 12$($\text{dm}$),高为$2× 2 = 4$($\text{dm}$)。
根据长方形面积公式$S_{长}=ab$(其中$a$为长,$b$为宽),可得大长方形面积为$12×8 = 96$($\text{dm}^2$)。
根据梯形面积公式可得梯形面积为$(4 + 8)×4÷2 = 24$($\text{dm}^2$)。
根据三角形面积公式可得三角形面积为$12×4÷2 = 24$($\text{dm}^2$)。
则空白部分面积为$24 + 24 = 48$($\text{dm}^2$)。
所以阴影部分面积$S = 96-48 = 48$($\text{dm}^2$)。
答案:$48\text{dm}^2$。
(1)
解析:本题考查组合图形的面积计算,可通过分割法将阴影部分分割成梯形和三角形,分别计算它们的面积,再将结果相加。
梯形的上底为$2× 4 = 8$($\text{dm}$),下底为$2× 2 = 4$($\text{dm}$),高为$2× 2 = 4$($\text{dm}$);三角形的底为$2× 2 = 4$($\text{dm}$),高为$2× 2 = 4$($\text{dm}$)。
根据梯形面积公式$S_1=(a + b)h÷2$(其中$a$为上底,$b$为下底,$h$为高),可得梯形面积为$(8 + 4)×4÷2 = 24$($\text{dm}^2$)。
根据三角形面积公式$S_2 = ah÷2$(其中$a$为底,$h$为高),可得三角形面积为$4×4÷2 = 8$($\text{dm}^2$)。
则阴影部分面积$S = S_1+S_2 = 24 + 8=32$($\text{dm}^2$)。
答案:$32\text{dm}^2$。
(2)
解析:本题考查不规则图形面积的计算,可采用添补法,用大长方形的面积减去空白部分的面积。
大长方形的长为$2× 6 = 12$($\text{dm}$),宽为$2× 4 = 8$($\text{dm}$);空白部分可看作一个梯形和一个三角形,梯形上底为$2× 2 = 4$($\text{dm}$),下底为$2× 4 = 8$($\text{dm}$),高为$2× 2 = 4$($\text{dm}$);三角形底为$2× 6 = 12$($\text{dm}$),高为$2× 2 = 4$($\text{dm}$)。
根据长方形面积公式$S_{长}=ab$(其中$a$为长,$b$为宽),可得大长方形面积为$12×8 = 96$($\text{dm}^2$)。
根据梯形面积公式可得梯形面积为$(4 + 8)×4÷2 = 24$($\text{dm}^2$)。
根据三角形面积公式可得三角形面积为$12×4÷2 = 24$($\text{dm}^2$)。
则空白部分面积为$24 + 24 = 48$($\text{dm}^2$)。
所以阴影部分面积$S = 96-48 = 48$($\text{dm}^2$)。
答案:$48\text{dm}^2$。
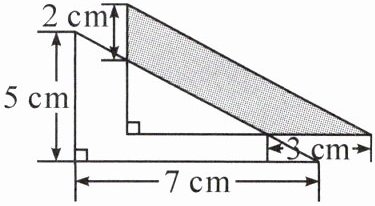
*5. 乐乐将 2 个完全相同的直角三角形叠放在一起(如图),阴影部分的面积是多少?

答案:
阴影部分面积等于下方梯形面积。
梯形上底:7 - 3 = 4(cm)
梯形面积:(4 + 7)×5÷2 = 27.5(cm²)
答:阴影部分的面积是27.5cm²。
梯形上底:7 - 3 = 4(cm)
梯形面积:(4 + 7)×5÷2 = 27.5(cm²)
答:阴影部分的面积是27.5cm²。
查看更多完整答案,请扫码查看


