1. 填空。
(1)一个三角形的底是 16 cm,高是 19 cm,与它等底等高的平行四边形的面积是
(2)一个直角三角形的三条边分别是 6 cm、8 cm、10 cm,它的面积是
(1)一个三角形的底是 16 cm,高是 19 cm,与它等底等高的平行四边形的面积是
304
$cm^2$。一个平行四边形的面积是$ 208 m^2,$与它等底等高的三角形的面积是104
$m^2$。 (2)一个直角三角形的三条边分别是 6 cm、8 cm、10 cm,它的面积是
24
$cm^2,$用这样的两个三角形拼成的平行四边形的面积是48
$cm^2。$
答案:
解析:
(1) 第一个空考查平行四边形的面积计算,公式为底乘以高。给定三角形的底和高与平行四边形等底等高,所以直接计算即可。
第二个空考查等底等高的三角形与平行四边形面积的关系,即等底等高的三角形面积是平行四边形面积的一半。
(2) 第三个空考查直角三角形的面积计算,由于已知两条直角边,所以面积等于两直角边乘积的一半。
第四个空考查用两个这样的三角形拼成的平行四边形的面积,即两个直角三角形的面积之和。
答案:
(1) $16 × 19 = 304(cm^2)$,所以与三角形等底等高的平行四边形的面积是$304 cm^2$。
$208 ÷ 2 = 104(m^2)$,所以与平行四边形等底等高的三角形的面积是$104 m^2$。
(2) $6 × 8 ÷ 2 = 24(cm^2)$,所以直角三角形的面积是$24 cm^2$。
$24 × 2 = 48(cm^2)$,所以用两个这样的三角形拼成的平行四边形的面积是$48 cm^2$。
(1) 第一个空考查平行四边形的面积计算,公式为底乘以高。给定三角形的底和高与平行四边形等底等高,所以直接计算即可。
第二个空考查等底等高的三角形与平行四边形面积的关系,即等底等高的三角形面积是平行四边形面积的一半。
(2) 第三个空考查直角三角形的面积计算,由于已知两条直角边,所以面积等于两直角边乘积的一半。
第四个空考查用两个这样的三角形拼成的平行四边形的面积,即两个直角三角形的面积之和。
答案:
(1) $16 × 19 = 304(cm^2)$,所以与三角形等底等高的平行四边形的面积是$304 cm^2$。
$208 ÷ 2 = 104(m^2)$,所以与平行四边形等底等高的三角形的面积是$104 m^2$。
(2) $6 × 8 ÷ 2 = 24(cm^2)$,所以直角三角形的面积是$24 cm^2$。
$24 × 2 = 48(cm^2)$,所以用两个这样的三角形拼成的平行四边形的面积是$48 cm^2$。
2. 判断。
(1)平行四边形的面积一定大于三角形的面积。(
(2)因为等底等高的三角形的面积相等,所以面积相等的三角形一定等底等高。(
(3)三条边分别相等的两个三角形一定能拼成一个平行四边形。(
(1)平行四边形的面积一定大于三角形的面积。(
×
) (2)因为等底等高的三角形的面积相等,所以面积相等的三角形一定等底等高。(
×
) (3)三条边分别相等的两个三角形一定能拼成一个平行四边形。(
√
)
答案:
解析:本题考查的是多边形面积的知识点。需要根据平行四边形、三角形面积的关系及图形的拼组知识进行判断。
(1)平行四边形的面积和三角形的面积大小取决于它们各自的底和高的长度,而不是它们的形状。
例如,一个底为2,高为1的平行四边形的面积是2,而一个底为4,高为3的三角形的面积是6,显然三角形的面积大于平行四边形的面积。
所以,“平行四边形的面积一定大于三角形的面积”是错误的。
答案:×。
(2)虽然等底等高的三角形面积相等,但面积相等的三角形不一定等底等高。
例如,一个底为4,高为3的三角形和一个底为6,高为2的三角形面积都是6,但它们的底和高并不相等。
所以,“面积相等的三角形一定等底等高”是错误的。
答案:×。
(3)如果两个三角形的三条边分别相等,那么这两个三角形是全等的。
当这两个全等的三角形以一组对应的边为公共边时,它们可以拼成一个平行四边形。
所以,“三条边分别相等的两个三角形一定能拼成一个平行四边形”是正确的。
答案:√。
(1)平行四边形的面积和三角形的面积大小取决于它们各自的底和高的长度,而不是它们的形状。
例如,一个底为2,高为1的平行四边形的面积是2,而一个底为4,高为3的三角形的面积是6,显然三角形的面积大于平行四边形的面积。
所以,“平行四边形的面积一定大于三角形的面积”是错误的。
答案:×。
(2)虽然等底等高的三角形面积相等,但面积相等的三角形不一定等底等高。
例如,一个底为4,高为3的三角形和一个底为6,高为2的三角形面积都是6,但它们的底和高并不相等。
所以,“面积相等的三角形一定等底等高”是错误的。
答案:×。
(3)如果两个三角形的三条边分别相等,那么这两个三角形是全等的。
当这两个全等的三角形以一组对应的边为公共边时,它们可以拼成一个平行四边形。
所以,“三条边分别相等的两个三角形一定能拼成一个平行四边形”是正确的。
答案:√。
3. 计算下面图形的面积。(单位:cm)


答案:
第一个图形:
根据直角三角形的面积公式 $S = \frac{1}{2}ah$,其中a为底,h为高。
代入数值:$S = \frac{1}{2} × 15 × 14 = 105({cm}^{2})$。
第二个图形:
同样使用直角三角形的面积公式 $S = \frac{1}{2}ah$。
代入数值:$S = \frac{1}{2} × 20 × 25 = 250({cm}^{2})$。
第三个图形:
使用直角三角形的面积公式 $S = \frac{1}{2}ah$。
代入数值:$S = \frac{1}{2} × 8.5 × 10 = 42.5({cm}^{2})$。
故答案为:$105{cm}^{2}$;$250{cm}^{2}$;$42.5{cm}^{2}$。
根据直角三角形的面积公式 $S = \frac{1}{2}ah$,其中a为底,h为高。
代入数值:$S = \frac{1}{2} × 15 × 14 = 105({cm}^{2})$。
第二个图形:
同样使用直角三角形的面积公式 $S = \frac{1}{2}ah$。
代入数值:$S = \frac{1}{2} × 20 × 25 = 250({cm}^{2})$。
第三个图形:
使用直角三角形的面积公式 $S = \frac{1}{2}ah$。
代入数值:$S = \frac{1}{2} × 8.5 × 10 = 42.5({cm}^{2})$。
故答案为:$105{cm}^{2}$;$250{cm}^{2}$;$42.5{cm}^{2}$。
4. 一块三角形指示牌,它的底是 9 dm,高是 8 dm,如果每平方米的材料费是 1500 元,那么制作这样一块指示牌需要多少材料费?
答案:
解析:本题考查三角形面积的计算以及单位换算。首先根据三角形面积公式计算出指示牌的面积,再将面积单位换算为平方米,最后根据每平方米的材料费计算出总费用。
答案:$三角形的面积 = 底×高÷2$
$9×8÷2$
$=72÷2$
$= 36({dm}^{2})$
$1{m}^{2} = 100{dm}^{2}$
$36{dm}^{2}=36÷100= 0.36{m}^{2}$
$材料费 = 面积×每平方米材料费$
$0.36×1500 = 540$(元)
答:制作这样一块指示牌需要540元材料费。
答案:$三角形的面积 = 底×高÷2$
$9×8÷2$
$=72÷2$
$= 36({dm}^{2})$
$1{m}^{2} = 100{dm}^{2}$
$36{dm}^{2}=36÷100= 0.36{m}^{2}$
$材料费 = 面积×每平方米材料费$
$0.36×1500 = 540$(元)
答:制作这样一块指示牌需要540元材料费。
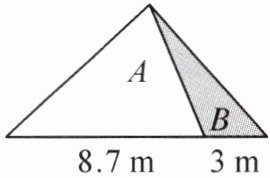
5. 如图,三角形 B 的面积是$ 12.6 m^2,$用于种菊花。三角形 A 种了绿草,它的底是 8.7 m,它的面积是多少平方米?

答案:
解析:本题可根据三角形面积公式以及两个三角形高相等的关系来求解三角形$A$的面积。
首先,根据三角形$B$的面积和底求出其高,由于三角形$A$和三角形$B$的高相等,再利用求出的高和三角形$A$的底来计算三角形$A$的面积。
已知三角形面积公式为$S = \frac{1}{2}ah$($S$表示面积,$a$表示底,$h$表示高)。
对于三角形$B$,已知其面积$S_{B}=12.6m^{2}$,底$a_{B}=3m$,将其代入面积公式可求出高$h$:
$12.6=\frac{1}{2}×3× h$
$h = 12.6×2÷3$
$h = 8.4$(米)
因为三角形$A$和三角形$B$的高相等,所以三角形$A$的高也是$8.4$米,又已知三角形$A$的底$a_{A}=8.7m$,再根据三角形面积公式可求出三角形$A$的面积$S_{A}$:
$S_{A}=\frac{1}{2}×8.7×8.4$
$S_{A}=36.54$(平方米)
答案:$36.54m^{2}$。
首先,根据三角形$B$的面积和底求出其高,由于三角形$A$和三角形$B$的高相等,再利用求出的高和三角形$A$的底来计算三角形$A$的面积。
已知三角形面积公式为$S = \frac{1}{2}ah$($S$表示面积,$a$表示底,$h$表示高)。
对于三角形$B$,已知其面积$S_{B}=12.6m^{2}$,底$a_{B}=3m$,将其代入面积公式可求出高$h$:
$12.6=\frac{1}{2}×3× h$
$h = 12.6×2÷3$
$h = 8.4$(米)
因为三角形$A$和三角形$B$的高相等,所以三角形$A$的高也是$8.4$米,又已知三角形$A$的底$a_{A}=8.7m$,再根据三角形面积公式可求出三角形$A$的面积$S_{A}$:
$S_{A}=\frac{1}{2}×8.7×8.4$
$S_{A}=36.54$(平方米)
答案:$36.54m^{2}$。
查看更多完整答案,请扫码查看


