1. 计算下面图形的面积。(单位:cm)


答案:
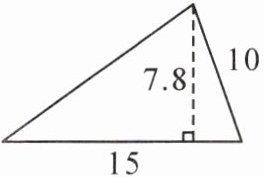
解析:本题主要考查三角形面积公式和梯形面积公式的应用。对于第一个图形是三角形,可根据三角形面积公式$S = ah÷2$(其中$a$为底,$h$为高)来计算其面积;对于第二个图形是梯形,可根据梯形面积公式$S=(a + b)h÷2$(其中$a$、$b$分别为上底和下底,$h$为高)来计算其面积。
答案:第一个图形:
$S=ah÷2$
$=15×7.8÷2$
$=117÷2$
$= 58.5$($cm^2$)
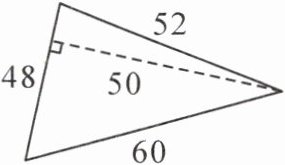
第二个图形:
$S=(a + b)h÷2$
$=(48 + 52)×50÷2$
$=100×50÷2$
$=5000÷2$
$= 2500$($cm^2$)
答案:第一个图形:
$S=ah÷2$
$=15×7.8÷2$
$=117÷2$
$= 58.5$($cm^2$)
第二个图形:
$S=(a + b)h÷2$
$=(48 + 52)×50÷2$
$=100×50÷2$
$=5000÷2$
$= 2500$($cm^2$)
| 图形 | 平行四边形 | | | 三角形 | | | |
| --- | --- | --- | --- | --- | --- | --- | --- |
| 底/m | 12.5 | 25 |
| 高/m | 9 |
| 面积$/m^{2}$ |
| --- | --- | --- | --- | --- | --- | --- | --- |
| 底/m | 12.5 | 25 |
4
| 5.6 | 5.2 | 5 | 6
|| 高/m | 9 |
16
| 3.2 | 2.4 | 4 | 3
| 5.2 || 面积$/m^{2}$ |
112.5
| 400 | 12.8 | 6.72
| 10.4
| 7.5 | 15.6 |
答案:
解析:本题主要考查平行四边形和三角形的面积计算。
平行四边形的面积公式为$S = a× h$($S$表示面积,$a$表示底,$h$表示高);
三角形的面积公式为$S = \frac{1}{2}× a× h$($S$表示面积,$a$表示底,$h$表示高)。
对于平行四边形:
已知底$a = 12.5m$,高$h = 9m$,根据面积公式可得面积$S=12.5× 9 = 112.5(m^{2})$。
已知底$a = 25m$,面积$S = 400m^{2}$,根据面积公式变形$h=\frac{S}{a}$,可得高$h = 400÷25 = 16(m)$。
已知高$h = 3.2m$,面积$S = 12.8m^{2}$,根据面积公式变形$a=\frac{S}{h}$,可得底$a = 12.8÷3.2 = 4(m)$。
对于三角形:
已知底$a = 5.6m$,高$h = 2.4m$,根据面积公式可得面积$S=\frac{1}{2}×5.6×2.4 = 6.72(m^{2})$。
已知底$a = 5.2m$,高$h = 4m$,根据面积公式可得面积$S=\frac{1}{2}×5.2×4 = 10.4(m^{2})$。
已知底$a = 5m$,面积$S = 7.5m^{2}$,根据面积公式变形$h=\frac{2S}{a}$,可得高$h = 2×7.5÷5 = 3(m)$。
已知底$a = 3m$,高$h = 2.6m$,根据面积公式可得面积$S=\frac{1}{2}×3×2.6 = 3.9(m^{2})$。
已知高$h = 5.2m$,面积$S = 15.6m^{2}$,根据面积公式变形$a=\frac{2S}{h}$,可得底$a = 2×15.6÷5.2 = 6(m)$。
答案:| 图形 | 平行四边形 | | | 三角形 | | | |
| --- | --- | --- | --- | --- | --- | --- | --- |
| 底/m | 12.5 | 25 | 4 | 5.6 | 5.2 | 5 | 6 |
| 高/m | 9 | 16 | 3.2 | 2.4 | 4 | 3 | 5.2 |
| 面积$/m^{2}$ | 112.5 | 400 | 12.8 | 6.72 | 10.4 | 7.5 | 15.6 |
平行四边形的面积公式为$S = a× h$($S$表示面积,$a$表示底,$h$表示高);
三角形的面积公式为$S = \frac{1}{2}× a× h$($S$表示面积,$a$表示底,$h$表示高)。
对于平行四边形:
已知底$a = 12.5m$,高$h = 9m$,根据面积公式可得面积$S=12.5× 9 = 112.5(m^{2})$。
已知底$a = 25m$,面积$S = 400m^{2}$,根据面积公式变形$h=\frac{S}{a}$,可得高$h = 400÷25 = 16(m)$。
已知高$h = 3.2m$,面积$S = 12.8m^{2}$,根据面积公式变形$a=\frac{S}{h}$,可得底$a = 12.8÷3.2 = 4(m)$。
对于三角形:
已知底$a = 5.6m$,高$h = 2.4m$,根据面积公式可得面积$S=\frac{1}{2}×5.6×2.4 = 6.72(m^{2})$。
已知底$a = 5.2m$,高$h = 4m$,根据面积公式可得面积$S=\frac{1}{2}×5.2×4 = 10.4(m^{2})$。
已知底$a = 5m$,面积$S = 7.5m^{2}$,根据面积公式变形$h=\frac{2S}{a}$,可得高$h = 2×7.5÷5 = 3(m)$。
已知底$a = 3m$,高$h = 2.6m$,根据面积公式可得面积$S=\frac{1}{2}×3×2.6 = 3.9(m^{2})$。
已知高$h = 5.2m$,面积$S = 15.6m^{2}$,根据面积公式变形$a=\frac{2S}{h}$,可得底$a = 2×15.6÷5.2 = 6(m)$。
答案:| 图形 | 平行四边形 | | | 三角形 | | | |
| --- | --- | --- | --- | --- | --- | --- | --- |
| 底/m | 12.5 | 25 | 4 | 5.6 | 5.2 | 5 | 6 |
| 高/m | 9 | 16 | 3.2 | 2.4 | 4 | 3 | 5.2 |
| 面积$/m^{2}$ | 112.5 | 400 | 12.8 | 6.72 | 10.4 | 7.5 | 15.6 |
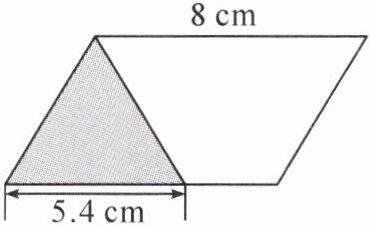
3. 如图,平行四边形的面积是$ 21.6 cm^2,$那么三角形的面积是多少?

答案:
平行四边形的高:21.6÷8=2.7(cm)
三角形的面积:5.4×2.7÷2=7.29(cm²)
答:三角形的面积是7.29cm²。
三角形的面积:5.4×2.7÷2=7.29(cm²)
答:三角形的面积是7.29cm²。
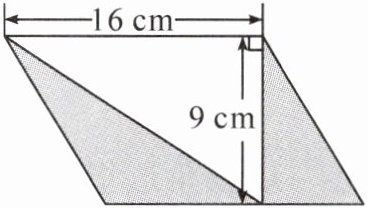
4. 右图中阴影部分的面积是多少平方厘米?

答案:
解析:本题可根据平行四边形的面积公式以及三角形与平行四边形面积的关系来求解阴影部分的面积。
从图中可知,阴影部分是一个三角形,该三角形与平行四边形等底等高。
根据平行四边形的面积公式$S = a× h$(其中$S$表示面积,$a$表示底,$h$表示高),可先求出平行四边形的面积,再根据等底等高的三角形面积是平行四边形面积的一半这一关系,求出阴影部分的面积。
已知平行四边形的底为$16$厘米,高为$9$厘米,则平行四边形的面积为:$16×9 = 144$(平方厘米)。
因为阴影部分三角形与平行四边形等底等高,所以阴影部分三角形的面积是平行四边形面积的一半,即:$144÷2 = 72$(平方厘米)。
答案:$72$平方厘米。
从图中可知,阴影部分是一个三角形,该三角形与平行四边形等底等高。
根据平行四边形的面积公式$S = a× h$(其中$S$表示面积,$a$表示底,$h$表示高),可先求出平行四边形的面积,再根据等底等高的三角形面积是平行四边形面积的一半这一关系,求出阴影部分的面积。
已知平行四边形的底为$16$厘米,高为$9$厘米,则平行四边形的面积为:$16×9 = 144$(平方厘米)。
因为阴影部分三角形与平行四边形等底等高,所以阴影部分三角形的面积是平行四边形面积的一半,即:$144÷2 = 72$(平方厘米)。
答案:$72$平方厘米。
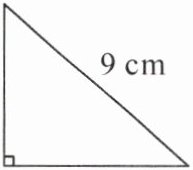
*5. 有一个等腰直角三角形,它的斜边长 9 cm,这个三角形的面积是多少平方厘米?

答案:
解析:本题可通过多种方法来求解等腰直角三角形的面积,以下用两种常见方法进行分析。
方法一:拼补法
把两个完全一样的等腰直角三角形拼成一个正方形,这个正方形的边长就是原等腰直角三角形的直角边,且正方形的面积是原等腰直角三角形面积的$2$倍。
设等腰直角三角形的直角边为$a$,根据勾股定理$a^{2}+a^{2}=9^{2}$(斜边的平方等于两直角边的平方和),即$2a^{2}=81$,那么$a^{2}=\frac{81}{2}$。
而三角形面积$S = \frac{1}{2}a^{2}$,将$a^{2}=\frac{81}{2}$代入可得$S=\frac{1}{2}×\frac{81}{2}=\frac{81}{4}= 20.25$平方厘米。
方法二:直接计算法
设等腰直角三角形的直角边为$x$厘米,根据勾股定理$x^{2}+x^{2}=9^{2}$,即$2x^{2}=81$,$x^{2}=\frac{81}{2}$。
根据三角形面积公式$S=\frac{1}{2}×底×高$,对于等腰直角三角形,底和高就是两条直角边,都为$x$,所以面积$S = \frac{1}{2}x^{2}$,把$x^{2}=\frac{81}{2}$代入可得$S=\frac{1}{2}×\frac{81}{2}=20.25$平方厘米。
答案:$20.25$平方厘米。
方法一:拼补法
把两个完全一样的等腰直角三角形拼成一个正方形,这个正方形的边长就是原等腰直角三角形的直角边,且正方形的面积是原等腰直角三角形面积的$2$倍。
设等腰直角三角形的直角边为$a$,根据勾股定理$a^{2}+a^{2}=9^{2}$(斜边的平方等于两直角边的平方和),即$2a^{2}=81$,那么$a^{2}=\frac{81}{2}$。
而三角形面积$S = \frac{1}{2}a^{2}$,将$a^{2}=\frac{81}{2}$代入可得$S=\frac{1}{2}×\frac{81}{2}=\frac{81}{4}= 20.25$平方厘米。
方法二:直接计算法
设等腰直角三角形的直角边为$x$厘米,根据勾股定理$x^{2}+x^{2}=9^{2}$,即$2x^{2}=81$,$x^{2}=\frac{81}{2}$。
根据三角形面积公式$S=\frac{1}{2}×底×高$,对于等腰直角三角形,底和高就是两条直角边,都为$x$,所以面积$S = \frac{1}{2}x^{2}$,把$x^{2}=\frac{81}{2}$代入可得$S=\frac{1}{2}×\frac{81}{2}=20.25$平方厘米。
答案:$20.25$平方厘米。
*6. 将一个三角形如右图所示剪拼成一个平行四边形,平行四边形的底是(
9
)cm,如果平行四边形的高是 a cm,那么三角形的面积是(9a
)cm²,剪拼后的平行四边形的周长是(2×(9+10)
)cm。
答案:
9;9a;2×(9+10)
查看更多完整答案,请扫码查看


