《2025年通成学典课时作业本九年级物理上册苏科版宿迁专版》

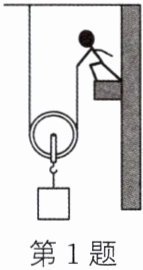
1. (2024·扬州)如图所示,工人用动滑轮匀速提升重为400N的窗玻璃,所用的竖直拉力为250N,窗玻璃上升的高度为10m,用时50s。求：
(1) 所做的有用功$W_{有用}$。
(2) 工人所用拉力的功率$P$。\n(3) 动滑轮的机械效率$\eta$。

答案： 【解析】：本题主要考查了有用功、总功、功率以及机械效率的计算，这些都是九年级物理中关于简单机械部分的重要知识点。
（1）有用功是直接对物体做的功，在提升重物的过程中，克服重物重力所做的功就是有用功，根据公式$W_{有}=Gh$（其中$G$是物体的重力，$h$是物体上升的高度）来计算。
（2）拉力的功率是拉力做功的快慢，需要先求出拉力做的总功，再根据功率公式$P = \frac{W}{t}$（其中$W$是总功，$t$是做功时间）来计算。对于动滑轮，绳子自由端移动的距离$s$与物体上升高度$h$的关系是$s = 2h$，总功$W_{总}=Fs$（其中$F$是拉力）。
（3）机械效率是有用功与总功的比值，根据公式$\eta=\frac{W_{有}}{W_{总}}×100\%$来计算。
【答案】：
(1)有用功是直接对窗玻璃做的功，根据公式$W_{有}=Gh$，已知$G = 400N$，$h = 10m$，则$W_{有}=400N×10m = 4000J$；
(2)使用动滑轮时，绳子自由端移动的距离$s = 2h = 2×10m = 20m$，拉力做的总功$W_{总}=Fs$，已知$F = 250N$，$s = 20m$，则$W_{总}=250N×20m = 5000J$，拉力的功率$P = \frac{W_{总}}{t}$，已知$t = 50s$，$W_{总}= 5000J$，则$P = \frac{5000J}{50s}=100W$；
(3)动滑轮的机械效率$\eta=\frac{W_{有}}{W_{总}}×100\%=\frac{4000J}{5000J}×100\% = 80\%$。
答：
(1)所做的有用功$W_{有}$为$4000J$；
(2)工人所用拉力的功率$P$为$100W$；
(3)动滑轮的机械效率$\eta$为$80\%$。

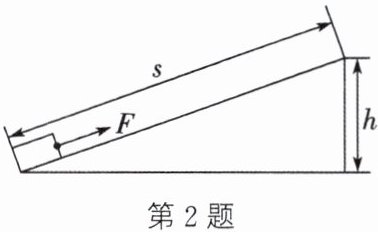
2. (2024·宿迁沭阳期中)如图,小明拉着质量为30kg的行李箱匀速经过一段长度$s= 3m$、高度$h= 1m$的斜坡路面,用时10s,若此过程拉力方向沿斜面向上,大小为125N。求：($g$取10N/kg)
- (1) 小明对行李箱做的有用功。\n(2) 斜面的机械效率。\n(3) 拉力$F$做功的功率。\n

答案： 【解析】：
本题主要考查了有用功、总功、机械效率以及功率的计算，知道使用斜面时克服重力做的功为有用功，拉力做的功为总功是解题的关键。
（1）行李箱的重力：$G = mg = 30× 10 = 300N$，
小明对行李箱做的有用功：$W_{有用} = Gh = 300× 1 = 300J$。
（2）拉力做的总功：$W_{总} = Fs = 125× 3 = 375J$，
斜面的机械效率：$\eta = \frac{W_{有用}}{W_{总}} × 100\% = \frac{300}{375} × 100\% = 80\%$。
（3）拉力$F$做功的功率：$P = \frac{W_{总}}{t} = \frac{375}{10} = 37.5W$。
【答案】：
（1）$300J$；（2）$80\%$；（3）$37.5W$。

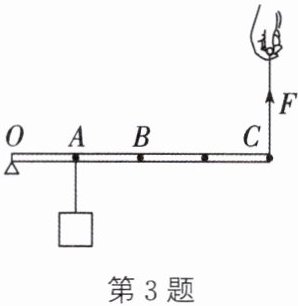
3. 如图所示为一根均匀的细木棒$OC$,$OA= \frac{1}{4}OC$,$B为OC$的中点。小明在$C点施加始终竖直向上的拉力F将挂在A$点的重为180N的物体匀速提升0.2m,细木棒的机械效率为90%,不计摩擦和绳子重。求：
- (1) 提升该物体做的有用功。\n(2) 拉力$F$所做的功。\n(3) 细木棒的重力。\n

答案：
(1)解：$W_{有}=Gh=180N×0.2m=36J$
(2)解：由$\eta=\frac{W_{有}}{W_{总}}$得，$W_{总}=\frac{W_{有}}{\eta}=\frac{36J}{90\%}=40J$
(3)解：设$OC=4L$，则$OA=L$，$OB=2L$，$C$点上升高度$h_{C}=2h=0.4m$，$B$点上升高度$h_{B}=h=0.2m$，额外功$W_{额}=W_{总}-W_{有}=40J - 36J=4J$，由$W_{额}=G_{木}h_{B}$得，$G_{木}=\frac{W_{额}}{h_{B}}=\frac{4J}{0.2m}=20N$