《2025年通成学典课时作业本九年级物理上册苏科版宿迁专版》

8. 用某滑轮组提升重物,已知重物和动滑轮的总重由5段绳子承担,绳重和摩擦不计,动滑轮共重20N。若在匀速提升重物时,绳端的拉力是100N,则被提升的重物的重力为 (B)
A.400N
B.480N
C.500N
D.520N

答案： B

9. 在水平桌面上放一个重为300N的物体,物体与桌面之间的摩擦力为60N,如图所示,若不考虑绳、滑轮的重力和绳的摩擦,则使物体以0.1m/s匀速移动时,水平拉力F和绳端移动速度的大小分别为 (D)
A.300N 0.1m/s
B.150N 0.1m/s
C.60N 0.2m/s
D.30N 0.2m/s

答案： D

10. 如图所示为手摇晾衣架的示意图,A、B两滑轮中属于动滑轮的是B,利用该滑轮能省力。若晾衣架和衣服的总重为100N,不计滑轮重、绳重及摩擦,将晾衣架和衣服匀速拉升的拉力F=25N。

答案： B 能 25

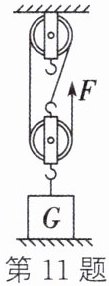
11. (2024·宿迁泗阳校级段考)如图所示的滑轮组,不计绳质量及滑轮转动摩擦。重物G= 100N,每一个滑轮重20N。当绳自由端拉力F竖直向上大小为30N时,重物G对地面的压力为30N。拉力F为40N时,恰能让重物G匀速上升。若重物G在10s内匀速上升了10cm,则绳自由端移动的距离为30cm,绳子自由端向上运动速度为0.03m/s。

答案： 30 40 30cm 0.03

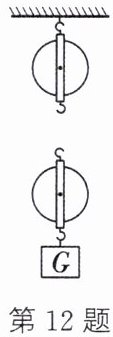
12. 用如图所示的滑轮组将一个G= 30N的物体用最省力的方法匀速提升10m。
(1) 请在图中画出最省力的滑轮组的绕绳方法。
(2) 绳端移动的距离是多大?
(3) 不计摩擦、绳重,实际拉力$F_1= 12N,$动滑轮的重G_{动}为多少?
(4) 不计摩擦、绳重,用此滑轮组提起G'= 114N的物体,实际拉力$F_2$为多少?

答案：
解：
（1）

（2）根据$s=nh$（$n$是绳子股数，$h$是物体上升高度），已知$n = 3$，$h = 10m$，则$s=3×10m = 30m$。
（3）不计摩擦、绳重，根据$F=\frac{1}{n}(G + G_{动})$，已知$F_1 = 12N$，$G = 30N$，$n = 3$，则$G_{动}=nF_1−G$，$G_{动}=3×12N−30N = 6N$。
（4）不计摩擦、绳重，根据$F=\frac{1}{n}(G + G_{动})$，$n = 3$，$G'=114N$，$G_{动}=6N$，则$F_2=\frac{1}{3}(G'+G_{动})=\frac{1}{3}(114N + 6N)=40N$。

13. 某同学用滑轮组提升物体,若物体升高1m时,绳子自由端移动的距离是3m,则该滑轮组承担物重的绳子的段数n=3,滑轮组至少由1个定滑轮和1个动滑轮组成。

答案： 3 1