第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
10. (2024·黔东南一模)阅读材料:
小明用配方法解一元二次方程 $2x^{2}+4x - 8 = 0$ 的过程如下:
解:移项,得 $2x^{2}+4x = 8$。…………第一步
二次项系数化为1,得 $x^{2}+2x = 4$。…………第二步
配方,得 $(x + 2)^{2}=8$。…………第三步
解这个方程,得 $x + 2=\pm2\sqrt{2}$。…………第四步
$\therefore x_{1}=-2 + 2\sqrt{2}$,$x_{2}=-2 - 2\sqrt{2}$。…………第五步
(1) 小明的解答过程从第
(2) 请写出正确的解答过程。
小明用配方法解一元二次方程 $2x^{2}+4x - 8 = 0$ 的过程如下:
解:移项,得 $2x^{2}+4x = 8$。…………第一步
二次项系数化为1,得 $x^{2}+2x = 4$。…………第二步
配方,得 $(x + 2)^{2}=8$。…………第三步
解这个方程,得 $x + 2=\pm2\sqrt{2}$。…………第四步
$\therefore x_{1}=-2 + 2\sqrt{2}$,$x_{2}=-2 - 2\sqrt{2}$。…………第五步
(1) 小明的解答过程从第
三
步开始出现错误;(2) 请写出正确的解答过程。
答案:
10.
(1) 三$ (2) 2x^2+4x-8=0,$移项,得$2x^2+4x=8. $二次项系数化为1,得$x^2+2x=4. $配方,得$(x+1)^2=5. $解这个方程,得$x+1=\pm\sqrt{5}.\therefore x_1=-1+\sqrt{5},x_2=-1-\sqrt{5}$
(1) 三$ (2) 2x^2+4x-8=0,$移项,得$2x^2+4x=8. $二次项系数化为1,得$x^2+2x=4. $配方,得$(x+1)^2=5. $解这个方程,得$x+1=\pm\sqrt{5}.\therefore x_1=-1+\sqrt{5},x_2=-1-\sqrt{5}$
11. 已知 $a$ 是不等式 $5(m - 2)+8\lt6(m - 1)+7$ 的最小整数解,请用配方法解关于 $x$ 的方程 $x^{2}+2ax + a + 1 = 0$。
答案:
11. 解不等式5(m-2)+8<6(m-1)+7,得m>$-3.\therefore $不等式的最小整数解为-2,即a=-2. 将a=-2代入方程$x^2+2ax+a+1=0,$得$x^2-4x-1=0. $配方,得$(x-2)^2=5. $解这个方程,得$x-2=\pm\sqrt{5}.\therefore x_1=2+\sqrt{5},x_2=2-\sqrt{5}$
12. (新考向·代数推理)阅读材料:
我们都知道 $a^{2}+2ab + b^{2}=(a + b)^{2}$,$a^{2}-2ab + b^{2}=(a - b)^{2}$。因此 $-2x^{2}+40x + 5=-2(x^{2}-20x)+5=-2(x^{2}-2\cdot x\cdot10 + 10^{2}-10^{2})+5=-2[(x - 10)^{2}-100]+5=-2(x - 10)^{2}+205$。$\because(x - 10)^{2}\geqslant0$,$\therefore - 2(x - 10)^{2}\leqslant0$。$\therefore - 2(x - 10)^{2}+205\leqslant205$。$\therefore - 2x^{2}+40x + 5$ 有最大值 205。
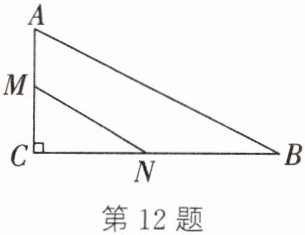
如图,在 $\triangle ABC$ 中,$\angle C = 90^{\circ}$,$AC = 4\mathrm{cm}$,$BC = 8\mathrm{cm}$,$M$、$N$ 分别是线段 $AC$ 和 $BC$ 上的动点,点 $M$ 从点 $A$ 出发以 $1\mathrm{cm/s}$ 的速度向点 $C$ 运动;同时点 $N$ 从点 $C$ 出发以 $2\mathrm{cm/s}$ 的速度向点 $B$ 运动,当其中一点到达终点时,两点同时停止运动。设运动的时间为 $t\mathrm{s}$,则当 $t$ 的值为多少时,$\triangle MCN$ 的面积最大?最大值为多少?
]
我们都知道 $a^{2}+2ab + b^{2}=(a + b)^{2}$,$a^{2}-2ab + b^{2}=(a - b)^{2}$。因此 $-2x^{2}+40x + 5=-2(x^{2}-20x)+5=-2(x^{2}-2\cdot x\cdot10 + 10^{2}-10^{2})+5=-2[(x - 10)^{2}-100]+5=-2(x - 10)^{2}+205$。$\because(x - 10)^{2}\geqslant0$,$\therefore - 2(x - 10)^{2}\leqslant0$。$\therefore - 2(x - 10)^{2}+205\leqslant205$。$\therefore - 2x^{2}+40x + 5$ 有最大值 205。
如图,在 $\triangle ABC$ 中,$\angle C = 90^{\circ}$,$AC = 4\mathrm{cm}$,$BC = 8\mathrm{cm}$,$M$、$N$ 分别是线段 $AC$ 和 $BC$ 上的动点,点 $M$ 从点 $A$ 出发以 $1\mathrm{cm/s}$ 的速度向点 $C$ 运动;同时点 $N$ 从点 $C$ 出发以 $2\mathrm{cm/s}$ 的速度向点 $B$ 运动,当其中一点到达终点时,两点同时停止运动。设运动的时间为 $t\mathrm{s}$,则当 $t$ 的值为多少时,$\triangle MCN$ 的面积最大?最大值为多少?
]

答案:
12. 由题意,得AM=t cm,CM=(4-t)cm,$CN=2t cm.\therefore S_{\triangle MCN}=\frac{1}{2}×2t\cdot(4-t)=-t^2+4t=[-(t-2)^2+4]cm^2.\because (t-2)^2\geq0,\therefore -(t-2)^2\leq0.\therefore -(t-2)^2+4\leq4.\therefore $当t=2时,$\triangle MCN$的面积最大,最大值为$4cm^2$
查看更多完整答案,请扫码查看


