《2025年金钥匙提优训练课课练九年级数学上册江苏版徐州专版》

7. 如图，△ABC 内接于⊙O，AB 是⊙O 的直径，延长 AB 到点 E，使得 BE = BC = 6，连接 EC，且∠ECB = ∠CAB，D 是$\overset{\frown}{AB}$上的点，连接 AD、CD，且 CD 交 AB 于点 F.
(1) 求证：EC 是⊙O 的切线；
(2) 若 CB 平分∠ECD，求 AD 的长.
]

答案： 7.
(1)连接OC.
∵OA=OC,
∴∠CAB=∠ACO.
∵∠ECB=∠CAB,
∴∠ECB=∠ACO.
∵AB是⊙O 的直径,
∴∠ACB=90°.
∴∠ACO+∠OCB=90°.
∴∠ECB+∠OCB=90°,即∠OCE=90°.
∴OC⊥EC.又
∵OC是⊙O的半径,
∴EC是⊙O的切线.
(2)
∵CB 平分∠ECD,
∴∠BCD=∠ECB.
∵∠BCD=∠BAD,
∴∠ECB=∠BAD.
∵∠ECB=∠CAB,
∴∠BAD=∠CAB.连接OD.
∵∠BOD=2∠BAD,∠COB=2∠CAB,
∴∠BOD=∠COB.又
∵OC=OD,
∴AB⊥DC.
∴∠ECF+∠E=90°.
∵BE=BC,
∴∠E=∠ECB.
∴∠E=∠ECB=∠BCF=30°.在Rt△BCF中,
∵BC=6,∠BCF=30°,
∴BF=$\frac{1}{2}$BC = 3.
∴由勾股定理,得CF = $\sqrt{BC^{2} - BF^{2}}$ = $\sqrt{6^{2} - 3^{2}}$ = 3$\sqrt{3}$.
∵AB⊥CD,AB是⊙O的直径,
∴DF = CF = 3$\sqrt{3}$.
∵∠DAF =∠BCF = 30°,
∴在Rt△ADF中,AD = 2DF = 6$\sqrt{3}$.

8. 如图，AB 为直径，且 AB = 6，将半圆绕点 B 顺时针旋转 30°，此时点 A 转到了点 A'处，则图中涂色部分的面积为(D)

A.$\frac{\pi}{2}$
B.$\frac{3\pi}{4}$
C.π
D.3π
]

答案： 8.D

9. 已知圆锥的母线长为 8 cm，侧面积为 24π cm²，则这个圆锥的底面圆的半径为3cm.

答案： 9.3

10. (2023·通辽)如图，在扇形 OAB 中，∠AOB = 60°，OD 平分∠AOB，交$\overset{\frown}{AB}$于点 D，C 是半径 OB 上一动点. 若 OA = 1，则图中涂色部分的周长的最小值为$\frac{\pi + 6\sqrt{2}}{6}$.

答案： 10.$\frac{\pi + 6\sqrt{2}}{6}$ 解析:作点D关于直线OB的对称点E,连接AE,交OB于点C,此时题图中涂色部分的周长最小,连接OE、DE.由OD平分∠AOB,得∠AOD = ∠BOD =$\frac{1}{2}$∠AOB = 30°.由轴对称的性质,得∠EOB = ∠BOD =30°,CE = CD,OE = OD,
∴∠AOE = 90°.
∵OA = OD,
∴OA = OE.
∴△AOE是等腰直角三角形.
∵OA = 1,
∴AE = $\sqrt{2}$,即AC + CD的最小值为$\sqrt{2}$.
∵$\overset\frown{AD}$的长为$\frac{30\pi × 1}{180}$ = $\frac{\pi}{6}$,
∴题图中涂色部分的周长的最小值为$\frac{\pi}{6}$ + $\sqrt{2}$ = $\frac{\pi + 6\sqrt{2}}{6}$.

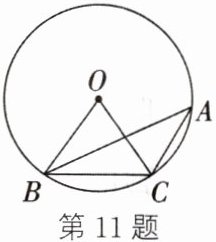
11. (2023·徐州模拟)如图，△ABC 是⊙O 的内接三角形，∠OBC = 55°，则∠A =35°.
]

答案： 11.35

12. (2023·徐州)如图，沿一条母线将圆锥的侧面剪开展平得到一个扇形. 若母线长 l 为 6 cm，扇形的圆心角 θ 为 120°，则圆锥底面圆的半径 r 为2cm.

答案： 12.2

13. (2024·徐州期末)如图，AB 是⊙O 的直径，弦 DE 与 AB 交于点 F，OD⊥AB，点 C 在 AB 的延长线上，连接 CE.
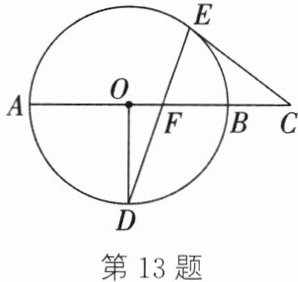
(1) 若 CF = CE，判断直线 CE 与⊙O 的位置关系，并说明理由；
(2) 若 AF = 4，DF = √{10}，求⊙O 的半径.
]

答案： 13.
(1)直线CE与⊙O相切.理由:连接OE.
∵OD⊥AB,
∴∠DOB = 90°.
∵CF = CE,OD = OE,
∴∠CEF =∠EFC,∠OED = ∠ODE.
∵∠OFD = ∠EFC,
∴∠OFD = ∠CEF.
∴∠OED + ∠CEF = ∠ODE +∠OFD = 180° - ∠DOB = 90°.
∴OE⊥CE.又
∵OE是⊙O的半径,
∴直线CE与⊙O相切.
(2)设⊙O的半径为r,则OD = r,OF = 4 - r.在Rt△DOF中,由勾股定理,得OD² + OF² = DF²,即r² + (4 - r)² = ($\sqrt{10}$)²,解得r₁ = 3,r₂ = 1(舍去).
∴⊙O的半径为3.