《2025年金钥匙提优训练课课练九年级数学上册江苏版徐州专版》

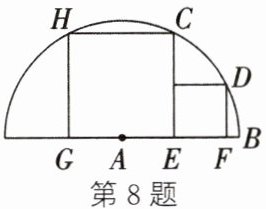
8. 如图,两个正方形彼此相邻且顶点H、C、D在半圆上.若小正方形的面积为16cm²,则半圆的半径为(C)
$A. (4+\sqrt{5})cm$
B. 9cm
$C. 4\sqrt{5}cm$
$D. 6\sqrt{2}cm$
]

答案：
8. C 解析:如图，连接AH、AC、AD.
∵ 四边形CEGH是正方形,
∴ ∠HGA = ∠CEA = 90°, HG = CE. 在Rt△HAG和Rt△CAE中，$\begin{cases} AH = AC, \\ HG = CE, \end{cases}$
∴ Rt△HAG ≌ Rt△CAE.
∴ AG = AE = $\frac{1}{2}$EG. 设大正方形的边长为2x cm，则AE = x cm, CE = 2x cm.
∵ 小正方形的面积为16 $cm^2$,
∴ EF = DF = 4 cm. 在Rt△AEC中，由勾股定理，得AE² + CE² = AC². 在Rt△AFD中，由勾股定理，得AF² + DF² = AD². 又
∵ AC = AD,
∴ $x^2 + (2x)^2 = (x + 4)^2 + 4^2$, 解得 $x_1 = 4, x_2 = -2$（不合题意, 舍去）.
∴ AE = 4 cm,
CE = 8 cm.
∴ 半圆的半径为 $\sqrt{4^2 + 8^2} = 4\sqrt{5}$(cm).

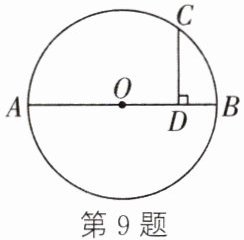
9. 如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D.若CD=4,BD=2,则AB=10.
]

答案：
9. 10 解析:如图，连接OC，设OC = x.
∵ OC = OB，BD = 2,
∴ OD = x - 2.
∵ CD ⊥ AB,
∴ ∠CDO = 90°. 在Rt△COD中，由勾股定理，得OC² = OD² + CD²，即 $x^2 = (x - 2)^2 + 4^2$，解得x = 5.
∴ OB = OC = 5.
∴ AB = 2OB = 10.

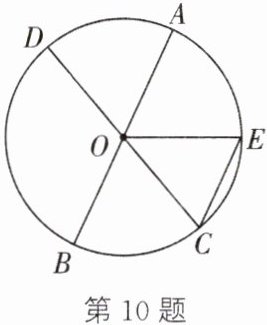
10. 如图,AB和CD为⊙O的两条直径,CE//AB交⊙O于点E,∠COE=50°.求∠BOD的度数.
]

答案： 10.
∵ OC = OE,
∴ ∠C = ∠E.
∵ ∠COE = 50°,
∴ ∠C = $\frac{1}{2} × (180° - \angle COE) = \frac{1}{2} × (180° - 50°) = 65°$.
∵ CE // AB,
∴ ∠AOD = ∠C = 65°.
∴ ∠BOD = 180° - 65° = 115°

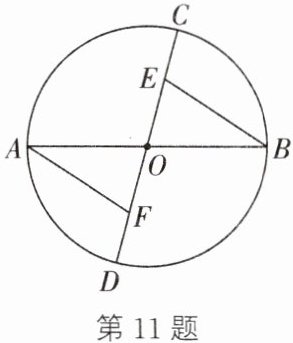
11. 如图,AB、CD为⊙O的两条直径,点E、F在CD上,且CE=DF.求证:AF=BE.
]

答案： 11.
∵ OC = OD, CE = DF,
∴ OC - CE = OD - DF，即OE = OF. 在△AOF和△BOE中，$\begin{cases} \angle AOF = \angle BOE, \\ OF = OE, \end{cases}$
∴ △AOF ≌ △BOE.
∴ AF = BE

12. 如图,直线l经过⊙O的圆心,且与⊙O交于A、B两点,点C在⊙O上,且∠AOC=30°,P是直线l上的一个动点(不与圆心O重合),直线CP与⊙O相交于另一点Q,连接QO.
(1) 当点P在半径OA上时,若QP=QO,求∠OCP的度数.
(2) 当点P在直线l上的其他位置时,是否还存在QP=QO? 若存在,请求出此时∠OCP的度数;若不存在,请说明理由.
]

答案：
12.
(1) 设 ∠QPO = x.
∵ QP = QO，
∴ ∠QPO = ∠QOP = x.
∴ ∠OQP = 180° - 2x.
∵ OC = OQ,
∴ ∠OCP = ∠OQC = 180° - 2x.
∵ ∠AOC = 30°，即∠POC = 30°, ∠QPO = ∠OCP + ∠POC,
∴ x = 180° - 2x + 30°, 解得x = 70°.
∴ ∠OCP = 180° - 2 × 70° = 40°
(2) 存在3种情况：① 如图①，当点P在OA的延长线上时，设 ∠QOC = y, 则 ∠QOP = y + 30°.
∵ QP = QO，
∴ ∠QPO = ∠QOP = y + 30°, 即 ∠CPO = y + 30°.
∴ ∠OCQ = ∠POC + ∠CPO = 30° + y + 30° = y + 60°.
∵ OQ = OC,
∴ ∠OQC = ∠OCQ = y + 60°.
∴ 在△OCQ中，根据三角形的内角和定理，得 ∠QOC + ∠OQC + ∠OCQ = 180°, 即 y + y + 60° + y + 60° = 180°, 解得y = 20°.
∴ ∠OCQ = 80°.
∴ ∠OCP = 180° - ∠OCQ = 100°.
② 如图②，当点P在OB的延长线上时，设 ∠QPO = z.
∵ QP = QO,
∴ ∠QPO = ∠QOP = z.
∴ ∠CQO = ∠QOP + ∠QPO = 2z.
∵ OC = OQ,
∴ ∠OCP = ∠CQO = 2z.
∵ ∠APC + ∠OCP = ∠AOC,
∴ z + 2z = 30°, 解得z = 10°.
∴ ∠OCP = 20°.
③ 当点P在线段OB上时，易知QP ≠ QO. 综上所述，∠OCP的度数为100°或20°