《2025年金钥匙提优训练课课练九年级数学上册江苏版徐州专版》

1. (2024·深圳期中)如图，在矩形 $ABCD$ 中，$AB = 8\mathrm{cm}$，$AD = 3\mathrm{cm}$，动点 $P$、$Q$ 同时出发，点 $P$ 从点 $A$ 出发以 $2\mathrm{cm}/\mathrm{s}$ 的速度向点 $B$ 移动，一直到达点 $B$ 为止，点 $Q$ 从点 $C$ 出发以 $1\mathrm{cm}/\mathrm{s}$ 的速度向点 $D$ 移动，则当点 $P$ 和点 $Q$ 的距离是 $5\mathrm{cm}$ 时，$P$、$Q$ 两点出发了(B)

A.$4\mathrm{s}$
B.$\frac{4}{3}\mathrm{s}$ 或 $4\mathrm{s}$
C.$\frac{8}{3}\mathrm{s}$ 或 $8\mathrm{s}$
D.$\frac{8}{3}\mathrm{s}$
]

答案： 1. B

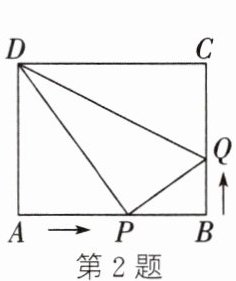
2. 如图，在矩形 $ABCD$ 中，$AB = 10\mathrm{cm}$，$AD = 8\mathrm{cm}$，点 $P$ 从点 $A$ 出发沿 $AB$ 以 $2\mathrm{cm}/\mathrm{s}$ 的速度向点 $B$ 运动，同时点 $Q$ 从点 $B$ 出发沿 $BC$ 以 $1\mathrm{cm}/\mathrm{s}$ 的速度向点 $C$ 运动，点 $P$ 到达终点后，$P$、$Q$ 两点同时停止运动. 当运动时间为2或3$\mathrm{s}$ 时，$\triangle BPQ$ 的面积是 $6\mathrm{cm}^2$.

答案： 2. 2或3

3. 如图，在矩形 $ABCD$ 中，$AB = 5\mathrm{cm}$，$BC = 6\mathrm{cm}$，点 $P$ 从点 $A$ 开始沿边 $AB$ 向终点 $B$ 以 $1\mathrm{cm}/\mathrm{s}$ 的速度运动，与此同时，点 $Q$ 从点 $B$ 开始沿边 $BC$ 向终点 $C$ 以 $2\mathrm{cm}/\mathrm{s}$ 的速度运动，当点 $Q$ 运动到点 $C$ 时，两点同时停止运动. 设运动时间为 $t\mathrm{s}(t ＞ 0)$.
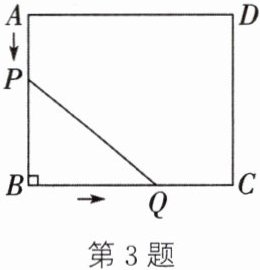
(1)填空：$BQ=$2t$\mathrm{cm}$，$PB=$5-t$\mathrm{cm}$(用含 $t$ 的代数式表示).
(2)当 $t$ 为何值时，$PQ$ 的长为 $5\mathrm{cm}$?
(3)是否存在 $t$ 的值，使得五边形 $APQCD$ 的面积等于 $26\mathrm{cm}^2$? 若存在，请求出此时 $t$ 的值；若不存在，请说明理由.
]

答案： 3.
(1) 2t (5-t)
(2) 由题意，得$(5-t)^{2}+(2t)^{2}=5^{2}$，解得$t_{1}=0$(不合题意，舍去)，$t_{2}=2$ $\therefore$当$t$的值为2时，PQ的长为$5cm$
(3) 存在$t$的值，使得五边形APQCD的面积等于$26 cm^2$ $\because$矩形ABCD的面积是$5×6 =$$30(cm^2)$，且五边形APQCD的面积等于$26 cm^2$，$\therefore\triangle PBQ$的面积为$30 - 26 = 4(cm^2)$ $\therefore(5 - t)\cdot2t×$$\frac{1}{2}=4$，解得$t_{1}=4$，$t_{2}=1$ $\because0＜t\leq3$，$\therefore t = 1$ $\therefore$当$t=$1时，五边形APQCD的面积等于$26 cm^2$

4. 如图，在一块长为 $36$ 米、宽为 $25$ 米的矩形空地上修建三条宽均为 $x$ 米的笔直小道，其余部分(即图中涂色部分)改造为草坪进行绿化，若草坪的面积为 $840$ 平方米，求 $x$ 的值. 根据题意，下列方程正确的是(D)

A.$36×25 - 36x - 25x = 840$
B.$36x + 25x = 840$
C.$(36 - x)(25 - x) + x^2 = 840$
D.$(36 - x)(25 - x) = 840$
]

答案： 4. D