《2025年金钥匙提优训练课课练九年级数学上册江苏版徐州专版》

1. (易错题)下列图形中,既是中心对称图形,又是轴对称图形的为 (C)
]

答案： 1.C　易错分析:易混淆轴对称图形与中心对称图形的识别方法.

2. (2023·邳州期中)如图,在正六边形 $ ABCDEF $ 中,$ \triangle ABD $ 的面积为 $ 4 $,则正六边形 $ ABCDEF $ 的面积为 (C)

A.$ 8 $
B.$ 10 $
C.$ 12 $
D.$ 14 $
]

答案： 2.C

3. 如图,在正五边形 $ ABCDE $ 中,对角线 $ AC $ 与 $ BE $ 相交于点 $ F $,则$ \angle AFE = $72$ ^{\circ} $.
]

答案： 3.72

4. 用一条宽度相等的足够长的纸条打一个结,然后轻轻拉紧、压平,就可以得到如图所示的正五边形 $ ABCDE $,则$ \angle BAC = $36$ ^{\circ} $.
]

答案： 4.36

5. (2023·沧州期中)如图,六边形 $ ABCDEF $ 是$ \odot O $ 的内接正六边形.
(1) 若$ \odot O $ 的半径为 $ 1 $,则六边形 $ ABCDEF $ 的周长为6；
(2) 设正六边形 $ ABCDEF $ 的面积为 $ S_{1} $,$ \triangle ACE $ 的面积为 $ S_{2} $,则$ \frac{S_{1}}{S_{2}} = $2.
]

答案：
5.
(1)6
(2)2　解析:如图，连接OA、OB、OC、OE.
∵六边形ABCDEF是⊙O的内接正六边形,
∴∠AOB=∠BOC=
$\frac{1}{6}$×360°=60°.
∵OA=OB=OC,
∴△OAB、△OBC是等边三角形.
∴OA=AB,OC=BC.在△OAC和△BAC中，$\begin{cases} OA = BA, \\ AC = AC, \\ OC = BC, \end{cases}$
∴△OAC≌△BAC.
∴$S_{\triangle OAC}=S_{\triangle BAC}$，由圆和正六边形的性质可得,$S_{\triangle BAC}=S_{\triangle AFE}=S_{\triangle CDE}$.由圆和正三角形的性质可得,$S_{\triangle OAC}=S_{\triangle OAE}=S_{\triangle OCE}$.
∵$S_1=S_{\triangle BAC}+S_{\triangle AFE}+S_{\triangle CDE}+S_{\triangle OAC}+S_{\triangle OAE}+S_{\triangle OCE}=6S_{\triangle OAC}$,$S_2=S_{\triangle OAC}+S_{\triangle OAE}+S_{\triangle ACE}=3S_{\triangle OAC}$,
∴$\frac{S_1}{S_2}=\frac{6S_{\triangle OAC}}{3S_{\triangle OAC}}=2$.
　　　　　　　　

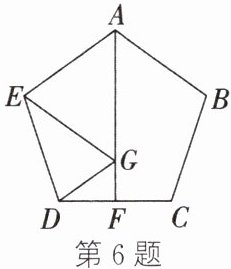
6. 如图,在正五边形 $ ABCDE $ 中,$ F $ 是 $ CD $ 的中点,点 $ G $ 在线段 $ AF $ 上运动,连接 $ EG $、$ DG $. 当 $ \triangle DEG $ 的周长最小时,$ \angle EGD $ 的度数为 (C)

A.$ 36^{\circ} $
B.$ 60^{\circ} $
C.$ 72^{\circ} $
D.$ 108^{\circ} $
]

答案： 6.C

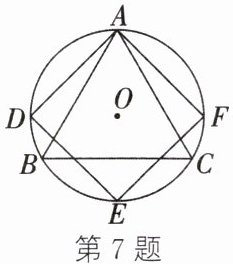
7. 如图,等边三角形 $ ABC $ 和正方形 $ ADEF $ 都内接于$ \odot O $,则 $ AD : AB $ 为 (B)

A.$ 2\sqrt{2} : \sqrt{3} $
B.$ \sqrt{2} : \sqrt{3} $
C.$ \sqrt{3} : \sqrt{2} $
D.$ \sqrt{3} : 2\sqrt{2} $
]

答案： 7.B

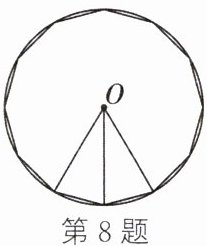
8. (2024·梧州一模)刘徽是我国魏晋时期卓越的数学家,他在《九章算术注》中提出了“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积. 如图,若用圆的内接正十二边形的面积 $ S_{1} $ 来近似估计$ \odot O $ 的面积 $ S $,设$ \odot O $ 的半径为 $ 1 $,则 $ S - S_{1} $ 的值为 (B)

A.$ \frac{\pi}{2} $
B.$ \pi - 3 $
C.$ 4 - \pi $
D.$ 2\pi - 5 $
]

答案：
8.B　解析:
∵⊙O的半径为1,
∴⊙O的面积S=π.如图，过点A作AC⊥OB于点C.
∵圆的内接正十二边形的中心角为$\frac{360^{\circ}}{12}$=30°,即∠AOC=30°,
∴AC=$\frac{1}{2}$OA=$\frac{1}{2}$.
∴圆的内接正十二边形的面积$S_1$=12×$\frac{1}{2}$×1×$\frac{1}{2}$=3.
∴$S - S_1$=π−3.