《2025年金钥匙提优训练课课练九年级数学上册江苏版徐州专版》

8. 如图，若小正方形的边长均为1，则$ \triangle ABC $的外心的坐标是(B)

A.$ (-1,-2) $
B.$ (-2,-1) $
C.$ (-2,-2) $
D.$ (-1,-1) $

答案： 8. B

9. 如图，将$ \triangle ABC $放在每个小正方形的边长均为1的网格中，点A、B、C均落在格点上，用一个圆面去覆盖$ \triangle ABC $，则能够完全覆盖这个三角形的最小圆面的半径是$\sqrt{5}$.

答案： 9. $\sqrt{5}$

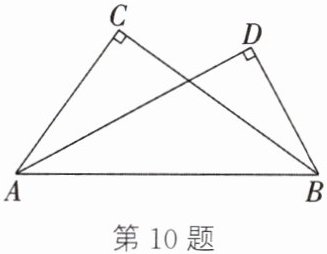
10. 如图，$ Rt \triangle ABC $与$ Rt \triangle ABD $有公共边AB，且点C、D在AB的同侧.设$ \odot O $是$ \triangle ABC $的外接圆.求证：点D在$ \odot O $上.

答案：
10. 如图，取AB的中点O，连接CO、DO.
∵ ∠ACB = 90°，O是AB的中点，
∴ OC = OA = OB = $\frac{1}{2}$AB.
∴ 点O是△ABC的外接圆的圆心. 又
∵ ∠ADB = 90°，
∴ OD = $\frac{1}{2}$AB = OA.
∴ 点D在⊙O上

11. （2023·金华一模）如图，点A、B、C在$ \odot O $上且$ AB = AC $，$ AB \perp AC $，请你利用直尺和圆规，用三种不同的方法找到圆心O（保留作图痕迹，不写作法）.

答案：
11. 画法不唯一，如图所示

12. 如图，点O在直线l上，过点O作$ AO \perp l $，$ AO = 3 $.P为直线l上一点，连接AP，在直线l右侧取点B，使$ \angle APB = 90^{\circ} $，且$ PA = PB $，过点B作$ BC \perp l $，交l于点C.
(1)求证：$ \triangle AOP \cong \triangle PCB $；
(2)若$ CO = 2 $，求BC的长；
(3)连接AB，若点C为$ \triangle ABP $的外心，则OP的长为3.

答案：
12.
(1)
∵ ∠APB = 90°，
∴ ∠APC + ∠CPB = 90°.
∵ AO⊥l，BC⊥l，
∴ ∠AOP = ∠PCB = 90°.
∴ ∠OAP + ∠APC = 90°.
∴ ∠OAP = ∠CPB. 在△AOP和△PCB中，$\begin{cases} \angle OAP = \angle CPB, \\ \angle AOP = \angle PCB, \end{cases}$
∴ △AOP ≌ △PCB (A.A)
(2)
∵ △AOP ≌ △PCB，
∴ AO = PC = 3，PO = BC.
∴ BC = PO = CO + PC = 2 + 3 = 5
(3) 3 解析：如图，若点C为△ABP的外心，则易知C是斜边AB的中点.
∵ BC⊥l，即AB⊥l，又
∵ AO⊥l，
∴ 点C与点O重合.
∵ PA = PB，∠APB = 90°，
∴ ∠A = ∠B = 45°.
∵ AO⊥l，
∴ ∠AOP = 90°.
∴ ∠APO = 90° - ∠A = 45°.
∴ ∠A = ∠APO.
∴ OP = AO.
∵ AO = 3，
∴ OP = 3.