《2025年金钥匙提优训练课课练九年级数学上册江苏版徐州专版》

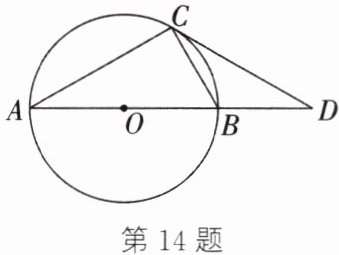
14. (2024·新沂模拟)如图，在⊙O 中，AB 是直径，C 是圆上一点，在 AB 的延长线上取一点 D，连接 CD，使∠BCD = ∠A.
(1) 求证：直线 CD 是⊙O 的切线；
(2) 若 AC = CD，DB = 2，求 AB 的长.
]

答案：
14.
(1)如图,连接OC.
∵OA = OC,
∴∠A = ∠ACO.
∵∠BCD = ∠A,
∴∠ACO = ∠BCD.
∵AB是⊙O的直径,
∴∠ACB = 90°.
∴∠ACO + ∠OCB = 90°.
∴∠BCD + ∠OCB = 90°,即∠OCD = 90°.
∴OC⊥CD.又
∵OC是⊙O的半径,
∴直线CD是⊙O的切线.
(2)
∵AC = CD,
∴∠A = ∠D.在△ACO和△DCB中,$\begin{cases} ∠A = ∠D, \\ AC = DC, \\ ∠ACO = ∠DCB, \end{cases}$
∴△ACO≌△DCB.
∴AO = DB = 2.
∴AB = 2AO = 4.

15. (2023·宿迁)在同一平面内，⊙O 的半径为 2，圆心 O 到直线 l 的距离为 3，P 为圆上的一个动点，则点 P 到直线 l 的最大距离是(B)

A.2
B.5
C.6
D.8

答案： 15.B

16. (转换法)(2024·连云港)如图，AB 是圆的直径，∠1、∠2、∠3、∠4 的顶点均在 AB 上方的圆弧上，∠1、∠4 的一边分别经过点 A、B，则∠1 + ∠2 + ∠3 + ∠4 =90°.
]

答案： 16.90

17. (2023·宿迁改编)若圆锥的底面圆的半径为 4 cm，侧面展开图是一个圆心角为 120°的扇

形

，则这个圆锥的母线长是12cm.

答案： 17.12

18. (2022·常州改编)现有若干张相同的半圆形纸片，点 O 是圆心，直径 AB 的长为 12 cm，C 是半圆上的一点(点 C 不与点 A、B 重合)，连接 AC、BC.
(1) 沿 AC、BC 剪下△ABC，则△ABC 是直角三角形(填“锐角”“直角”或“钝角”).
(2) 分别取半圆上的点 E、F 和直径 AB 上的点 G、H. 已知剪下的由这四个点顺次连接构成的四边形是一个边长为 6 cm 的菱形. 请用直尺和圆规在图中作出一个符合条件的菱形(保留作图痕迹，不写作法).
]

答案：
18.
(1)直角
(2)如图,四边形EFHG或四边形EFG'H即为所求.