《2025年金钥匙提优训练课课练九年级数学上册江苏版徐州专版》

11. (2024·张掖期中)先阅读理解下面的例题，再按要求解答下面的问题：
例题：求代数式$y^{2}+4y + 8$的最小值.
解：$y^{2}+4y + 8 = y^{2}+4y + 4 + 4 = (y + 2)^{2}+4$. $\because (y + 2)^{2}\geq0$，$\therefore (y + 2)^{2}+4\geq4$. $\therefore y^{2}+4y + 8$的最小值是4.
(1)求代数式$m^{2}+m + 4$的最小值；
(2)求代数式$4 - x^{2}+2x$的最大值.

答案： 11.
(1) $m^2+m+4=m^2+m+(\frac{1}{2})^2+\frac{15}{4}=(m+\frac{1}{2})^2+\frac{15}{4}$。$\because (m+\frac{1}{2})^2 \geq 0$，$\therefore (m+\frac{1}{2})^2+\frac{15}{4} \geq \frac{15}{4}$。$\therefore m^2+m+4$的最小值为$\frac{15}{4}$。
(2) $4 - x^2 + 2x = -(x^2 - 2x + 1) + 5 = -(x - 1)^2 + 5$。$\because -(x - 1)^2 \leq 0$，$\therefore -(x - 1)^2 + 5 \leq 5$。$\therefore 4 - x^2 + 2x$的最大值为5。

12. 若一个直角三角形的三边长分别为$a$、$b$、$c$，且两直角边长$a$、$b$满足$(a^{2}+b^{2})^{2}-2(a^{2}+b^{2})-15 = 0$，求斜边长$c$.

答案： 12. $\because (a^2 + b^2)^2 - 2(a^2 + b^2) - 15 = 0$，$\therefore (a^2 + b^2 - 1)^2 = 16$。$\therefore a^2 + b^2 - 1 = \pm 4$。$\therefore a^2 + b^2 = 5$或$a^2 + b^2 = -3$。又$\because a^2 + b^2 ＞ 0$，$\therefore a^2 + b^2 = 5$。$\therefore$由勾股定理，得$c = \sqrt{a^2 + b^2} = \sqrt{5}$。

13. (新考向·数学文化)阅读材料：
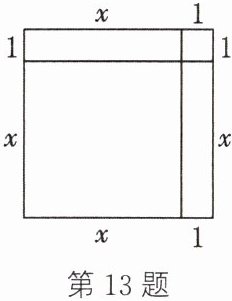
著名数学家花剌子米被誉为“代数之父”.他利用正方形图形巧妙解出了一元二次方程$x^{2}+2x - 35 = 0$的一个正数解.他的构思如图所示，将边长为$x$的正方形、边长为1的正方形和两个长为$x$、宽为1的矩形拼合在一起，拼成的大正方形的面积是$x^{2}+2\cdot x\cdot1 + 1^{2}$，即$x^{2}+2x + 1$，而由原方程$x^{2}+2x - 35 = 0$变形得$(x + 1)^{2}=36$，即边长为$x + 1$的正方形的面积为36.由于面积为36的正方形的边长为6，因此$x + 1 = 6$，则$x = 5$.
(1)材料中所体现的最主要的数学思想方法是B；
A. 分类讨论思想
B. 数形结合思想
C. 转化思想
D. 整体思想
(2)仿照上述方法构造出符合方程$x^{2}+6x - 7 = 0$的一个正数解的正方形(画出拼成的大正方形并求出正数解).

答案：
13.
(1) B　
(2) 如图，将边长为x的正方形、边长为3的正方形和两个长为3、宽为x的矩形拼合在一起，拼成的大正方形的面积是$x^2 + 2 \cdot x \cdot 3 + 3^2$，即$x^2 + 6x + 9$，而由原方程$x^2 + 6x - 7 = 0$变形得$(x + 3)^2 = 16$，即边长为$x + 3$的正方形的面积为16。$\because$面积为16的正方形的边长为4，$\therefore x + 3 = 4$。$\therefore$正数解为$x = 1$。