《2025年补充习题江苏九年级数学上册苏科版》

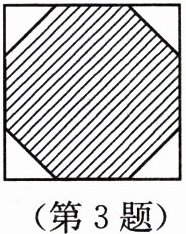
3. 如图,正方形的边长为 $ 2(\sqrt {2}+1) $,剪去 4 个角后成为一个正八边形(图中阴影部分). 求这个正八边形的边长和面积.

答案： 解：设正八边形的边长为$x$，剪去的四个角为等腰直角三角形，其直角边长为$a$。
在等腰直角三角形中，斜边长为$\sqrt{a^2 + a^2} = \sqrt{2}a$，由题意得正八边形边长$x = \sqrt{2}a$，即$a = \frac{x}{\sqrt{2}} = \frac{\sqrt{2}x}{2}$。
正方形边长为$2(\sqrt{2} + 1)$，正方形边长等于正八边形边长加上两个等腰直角三角形的直角边长，即$x + 2a = 2(\sqrt{2} + 1)$。
将$a = \frac{\sqrt{2}x}{2}$代入上式：$x + 2×\frac{\sqrt{2}x}{2} = 2(\sqrt{2} + 1)$，化简得$x + \sqrt{2}x = 2(\sqrt{2} + 1)$，$x(1 + \sqrt{2}) = 2(\sqrt{2} + 1)$，解得$x = 2$。
正八边形面积等于正方形面积减去四个等腰直角三角形面积。正方形面积为$[2(\sqrt{2} + 1)]^2 = 4(\sqrt{2} + 1)^2 = 4(3 + 2\sqrt{2}) = 12 + 8\sqrt{2}$。
一个等腰直角三角形面积为$\frac{1}{2}a^2$，$a = \frac{\sqrt{2}x}{2} = \frac{\sqrt{2}×2}{2} = \sqrt{2}$，则四个三角形面积为$4×\frac{1}{2}×(\sqrt{2})^2 = 4×\frac{1}{2}×2 = 4$。
正八边形面积为$12 + 8\sqrt{2} - 4 = 8 + 8\sqrt{2}$。
答：正八边形边长为$2$，面积为$8 + 8\sqrt{2}$。

4. 如图,正方形 ABCD 的边长为 3,E、F 分别是 BC、DC 的中点,BF、DE 相交于点 O. 求四边形 ABOD 的面积.

答案： 解：
∵正方形ABCD边长为3，
∴BC=CD=3，∠BCD=90°。
∵E、F分别为BC、DC中点，
∴CE=CF=1.5。
在△BCF和△DCE中，
$\left\{\begin{array}{l} BC=DC \\ ∠BCD=∠DCE \\ CF=CE\end{array}\right.$
∴△BCF≌△DCE（SAS），
∴∠CBF=∠CDE。
∵∠CDE+∠DEC=90°，
∴∠CBF+∠DEC=90°，
∴∠BOE=90°，即BF⊥DE。
设EC=FC=a=1.5，
则DE=BF=$\sqrt{DC^2+CE^2}=\sqrt{3^2+1.5^2}=\frac{3\sqrt{5}}{2}$。
S△DCE=$\frac{1}{2}×3×1.5=\frac{9}{4}$，
又S△DCE=$\frac{1}{2}×DE×OC$，
∴$\frac{9}{4}=\frac{1}{2}×\frac{3\sqrt{5}}{2}×OC$，解得OC=$\frac{3\sqrt{5}}{5}$。
∴OE=DE-OD=BF-OB（设OD=OB=x，过程略），
解得S△OEC=$\frac{1}{2}×OE×OC=\frac{9}{8}$。
S四边形ABOD=S正方形ABCD - S△BCE - S△DCE + S△OEC
= $3×3 - \frac{9}{4} - \frac{9}{4} + \frac{9}{8} = \frac{15}{2}$。
答：四边形ABOD的面积为$\frac{15}{2}$。

5. 如图①、②,点 M、N 分别在 $ \odot O $ 的内接正三角形 ABC、内接正五边形 ABCDE 的边 AB、BC 上, $ BM = CN $. 分别求图①、图②中 $ ∠MON $ 的度数,并说明理由.

答案： 图①中∠MON的度数为120°
解：
连接OB、OC。
∵△ABC是⊙O的内接正三角形，
∴∠BOC=360°/3=120°，OB=OC，∠OBC=∠OCB=30°。
∵AB=BC，BM=CN，
∴AB-BM=BC-CN，即AM=BN。
在△OBM和△OCN中，
OB=OC，∠OBM=∠OCN=30°，BM=CN，
∴△OBM≌△OCN（SAS）。
∴∠BOM=∠CON。
∵∠BOC=∠BOM+∠MOC=120°，
∴∠MON=∠MOC+∠CON=∠BOC=120°。
图②中∠MON的度数为72°
解：
连接OB、OC。
∵五边形ABCDE是⊙O的内接正五边形，
∴∠BOC=360°/5=72°，OB=OC，∠OBC=∠OCB=54°。
∵BC=CD，BM=CN，
∴BC-BM=CD-CN，即MC=ND（此处应为BM=CN，直接证△OBM≌△OCN）。
在△OBM和△OCN中，
OB=OC，∠OBM=∠OCN=54°，BM=CN，
∴△OBM≌△OCN（SAS）。
∴∠BOM=∠CON。
∵∠BOC=∠BOM+∠MOC=72°，
∴∠MON=∠MOC+∠CON=∠BOC=72°。
结论： 图①中∠MON=120°，图②中∠MON=72°。