《2025年暑假作业教育科学出版社七年级数学广西专版》

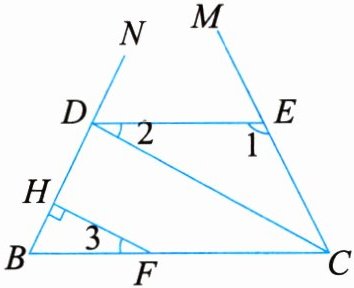
14. 如图所示,已知$CD平分\angle MCB$,点$F在线段BC$上,$FH\perp NB于点H$,$\angle 1 = 132^{\circ}$,$\angle 2 = \angle 3$,$\angle MCB = 48^{\circ}$.
(1)求证：$NB\perp CD$；
(2)求$\angle NDE$的度数.

答案： 1. （1）证明$NB\perp CD$：
解：
因为$CD$平分$\angle MCB$，$\angle MCB = 48^{\circ}$，根据角平分线定义$\angle DCB=\frac{1}{2}\angle MCB$，所以$\angle DCB=\frac{1}{2}×48^{\circ}=24^{\circ}$。
又因为$\angle 2=\angle 3$，$FH\perp NB$，即$\angle FHB = 90^{\circ}$，且$\angle 1 = 132^{\circ}$，$\angle 1+\angle DEC=180^{\circ}$（邻补角定义），所以$\angle DEC = 180^{\circ}-\angle 1=180 - 132^{\circ}=48^{\circ}$。
因为$\angle DEC$是$\triangle DCB$的外角（外角定义），根据三角形外角性质$\angle DEC=\angle 2+\angle DCB$，又$\angle 2=\angle 3$，所以$\angle 3+\angle DCB=\angle DEC$。
设$\angle 2 = \angle 3=x$，则$x + 24^{\circ}=48^{\circ}$，解得$x = 24^{\circ}$，即$\angle 3 = 24^{\circ}$。
在$\triangle BCH$中，$\angle BHC=180^{\circ}-(\angle 3+\angle DCB)-\angle FHB$（三角形内角和为$180^{\circ}$），$\angle 3+\angle DCB = 48^{\circ}$，$\angle FHB = 90^{\circ}$，所以$\angle BHC = 90^{\circ}$，即$NB\perp CD$。
2. （2）求$\angle NDE$的度数：
解：
因为$NB\perp CD$，$FH\perp NB$，所以$CD// FH$（垂直于同一条直线的两条直线平行）。
所以$\angle NDC=\angle 3 = 24^{\circ}$（两直线平行，同位角相等）。
又因为$\angle NDE+\angle NDC = 180^{\circ}$（邻补角定义）。
所以$\angle NDE=180^{\circ}-\angle NDC$，把$\angle NDC = 24^{\circ}$代入得$\angle NDE=180 - 24^{\circ}=156^{\circ}$。
综上，（1）得证$NB\perp CD$；（2）$\angle NDE$的度数为$156^{\circ}$。

15. 如图1所示,在一张正方形纸片(正方形的两组对边分别平行)的两边上分别有A,B两点,连接AB,点P是正方形纸片上一点,过点P翻折纸片,使点B落在直线AB上的点B'处,折痕MN交AB于点Q.
(1)①判断折痕MN与AB的位置关系,并说明理由；
②通过不断地尝试,除了上面的折法,过点P再也折不出其他与AB有①中位置关系的折痕,其中的数学道理是在同一平面内，过一点有且只有一条直线与已知直线垂直；
(2)在图1的基础上,展平纸片,得到图2,在图2中过点P折出并画出与AB平行的折痕DE(折痕左端点记为点D,右端点记为点E),请简要阐述折叠方法并说明理由；
折叠方法：过点P折叠纸片，使点Q落在MN上（除P点外）的某一点H处，折痕为DE。
理由：因为MN⊥AB，由折叠可知DE⊥MN（折叠前后对应线段垂直），根据“在同一平面内，垂直于同一条直线的两条直线互相平行”，所以DE// AB。
(3)将图2的纸片展平得到图3,点S是线段FG上一动点(不与点E重合),若∠DEF = 26°,∠EDS = α,∠CAS = β,请直接写出∠DSA的度数.(用α,β的代数式表示)
∠DSA=α+β - 26°

答案： 1. （1）
①
解：$MN\perp AB$。
理由：由折叠可知，$MN$是线段$BB'$的垂直平分线，$\angle BQM=\angle B'QM = 90^{\circ}$，所以$MN\perp AB$。
②
答案：在同一平面内，过一点有且只有一条直线与已知直线垂直。
2. （2）
折叠方法：过点$P$折叠纸片，使点$Q$落在$MN$上（除$P$点外）的某一点$H$处，折痕为$DE$。
理由：因为$MN\perp AB$，由折叠可知$DE\perp MN$（折叠前后对应线段垂直），根据“在同一平面内，垂直于同一条直线的两条直线互相平行”，所以$DE// AB$。
3. （3）
答案：$\angle DSA=\alpha+\beta - 26^{\circ}$或$\angle DSA = \alpha+\beta-26°$