《2025年名校课堂七年级数学上册人教版江西专版》

14. 三个队种树，第一队种树$x$棵，第二队种的树比第一队种的树的$2$倍还多$8$棵，第三队种的树比第二队种的树的一半少$6$棵，则三个队共种树A棵.

答案： A

15. 某超市在“双十一”期间对顾客购物实行优惠，规定如下：

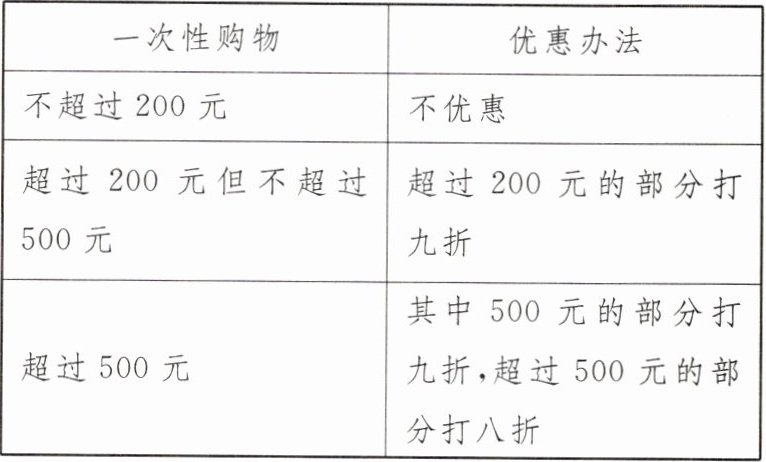
(1) 若王阿姨一次性购物$400$元，则实际付款380元；若一次性购物$600$元，则实际付款530元.
(2) 若王阿姨在该超市一次性购物$x$元，当$x$超过$200$但不超过$500$时，她实际付款(0.9x+20)元；当$x$超过$500$时，她实际付款(0.8x+50)元.
(3) 如果王阿姨两次购物合计$820$元，且第一次购物的货款为$a$元$(200 ＜ a ＜ 300)$，用含$a$的代数式表示若王阿姨一次性购这$820$元物品比分两次购会省多少元.

答案： 15. 解:
(1)380 530
(2)$(0.9x+20)$ $(0.8x+50)$
(3)根据题意,得第二次购物的货款为$(820-a)$元,$\because 200\lt a\lt 300,\therefore 520\lt 820-a\lt 620$.一次性购这820元物品:付款$0.9×500+0.8×(820-500)=706$(元);分两次购820元:实际付款第一次购物实际付款$(0.9a+20)$元,第二次购物实际付款$0.9×500+0.8×[(820-a)-500]=(706-0.8a)$元,两次购物总共实际付款$(0.9a+20)+(706-0.8a)=(0.1a+726)$元.$(0.1a+726)-706=(0.1a+20)$元.
答:王阿姨一次性购这820元物品比分两次购会省$(0.1a+20)$元.

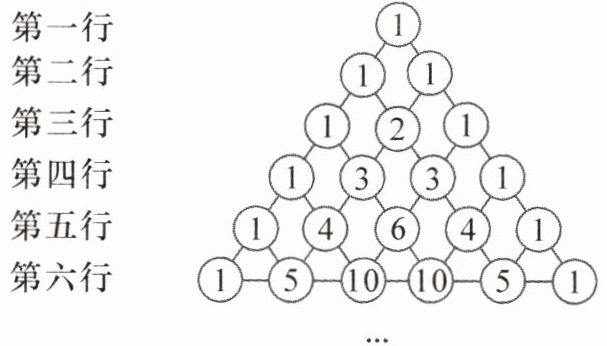
16. 新考向 数学文化 在我国南宋数学家杨辉所著的《详解九章算法》(1261 年)一书中，用如图所示的三角形解释二项和的乘方规律，因此我们称这个三角形为“杨辉三角”. 根据规律，第八行从左到右第三个数为21.

答案： 21

17. 新考向 推理能力 “歌唱家在家唱歌”“蜜蜂酿蜂蜜”这两句话从左往右读和从右往左读，结果完全相同，文学上把这样的现象称为“回文”. 数学上也有类似的“回文数”，比如$252$，$7887$，$34143$. 小明在计算两位数减法的过程中意外地发现，有些等式从左往右读的结果和从右往左读的结果一样，例如：$65 - 38 = 83 - 56$；$91 - 37 = 73 - 19$；$54 - 36 = 63 - 45$. 数学上把这类等式叫作“减法回文等式”.
(1) 观察以上等式，请再写出一个“减法回文等式”.
(2) 请归纳“减法回文等式”的被减数$\overline{ab}$(十位数字为$a$，个位数字为$b$)与减数$\overline{cd}$应满足的条件，并说明理由.

答案： 17. 解:
(1)$81-72=27-18$(答案不唯一).
(2)“减法回文等式”的被减数$\overline{ab}$(十位数字为$a$,个位数字为$b$)与减数$\overline{cd}$应满足的条件是$a-c=d-b$.理由:$\because \overline{ab}-\overline{cd}=\overline{dc}-\overline{ba}$,即$10a+b-(10c+d)=10d+c-(10b+a)$,$\therefore 10a+b-10c-d=10d+c-10b-a$,$\therefore 11a+11b=11c+11d$,$\therefore a+b=c+d$,$\therefore a-c=d-b$.