第43页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
9. 计算: $-2^2 × \frac{1}{4} ÷ (- \frac{1}{2})^2 × (-2)^3$.
答案:
9.解:原式=-4×$\frac{1}{4}$÷$\frac{1}{4}$×(-8)=4×$\frac{1}{4}$×4×8=32.
10.$(2024 \cdot 甘肃)$定义一种新运算“$*$”,规定运算法则为$m * n = m^n - mn$($m,n$均为整数,且$m \neq 0$). 例如: $2 * 3 = 2^3 - 2 × 3 = 2$. 则$(-2) * 2 =$
8
.
答案:
10.8
11. 如图,这是一个简单的数值运算程序. 当输入$x$的值为$-1$时,输出的数值为
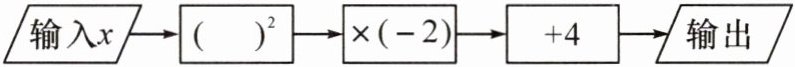
输入$x$→$(
2
.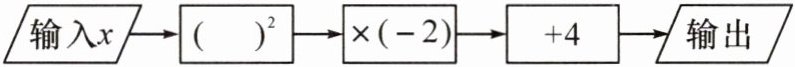
输入$x$→$(
x
)^2$→$× (-2)$→$\underline{\quad\quad}$+4→输出
答案:
11.2
12. 近年来,绿色低碳的骑行活动受到年轻人的青睐,一句“青春没有售价,夜骑开封拿下”成功吸引了数万名郑州的大学生夜骑共享单车到开封. 共享单车的开关两种状态可以用二进制中的1和0两个数字表示,约定逢二进一, 二进制数101转化为十进制数的方法为: 从右起, 第一位上的1表示$1 × 2^0$, 第二位上的0表示$0 × 2^1$, 第三位上的1表示$1 × 2^2$, 故二进制数101转化为十进制数为$1 × 2^0 + 0 × 2^1 + 1 × 2^2 = 5$ (规定$2^0 = 1$),则二进制数1011001转化为十进制数是
89
.
答案:
12.89
13. 计算:
(1)$-1^2 - (1 - \frac{1}{3}) ÷ 3 × (- \frac{3}{2})^2$.
(2)$-2^4 + |-5| - [-(-3) ÷ \frac{1}{6} + 2]$.
(1)$-1^2 - (1 - \frac{1}{3}) ÷ 3 × (- \frac{3}{2})^2$.
(2)$-2^4 + |-5| - [-(-3) ÷ \frac{1}{6} + 2]$.
答案:
13.解:
(1)原式=-1-$\frac{2}{3}$×$\frac{1}{3}$×$\frac{9}{4}$=-1-$\frac{1}{2}$=-1$\frac{1}{2}$.
(2)原式=-16+5-(3×6+2)=-16+5-20=-31.
(1)原式=-1-$\frac{2}{3}$×$\frac{1}{3}$×$\frac{9}{4}$=-1-$\frac{1}{2}$=-1$\frac{1}{2}$.
(2)原式=-16+5-(3×6+2)=-16+5-20=-31.
14. 已知$a, b, c$都是有理数,$a^2 = 9$, $|b| = 4$, $c^3 = 27$, 且$ab < 0$, $bc > 0$, 求式子$ab - bc + ca$的值.
答案:
14.解:由题意,得a=±3,b=±4,c=3.
∵ab<0,bc>0,
∴c=3,b=4,a=-3.
∴原式=-3×4-4×3+3×(-3)=-12-12-9=-33.
∵ab<0,bc>0,
∴c=3,b=4,a=-3.
∴原式=-3×4-4×3+3×(-3)=-12-12-9=-33.
15. [新考向 推理能力] 观察下面三行数:
$2, -4, 8, -16, \cdots$; ①
$-1, 2, -4, 8, \cdots$; ②
$3, -3, 9, -15, \cdots$; ③
(1) 第①行的数按如下规律排列:
$2^1$, $\underline{\quad\quad}$, $\underline{\quad\quad}$, $\underline{\quad\quad}$, $\cdots$.
(2) 第②③行的数与第①行的数分别有什么关系?
(3) 取每行数的第9个数,计算这三个数的和.
$2, -4, 8, -16, \cdots$; ①
$-1, 2, -4, 8, \cdots$; ②
$3, -3, 9, -15, \cdots$; ③
(1) 第①行的数按如下规律排列:
$2^1$, $\underline{\quad\quad}$, $\underline{\quad\quad}$, $\underline{\quad\quad}$, $\cdots$.
-2⁵ 2⁶ -2⁷
(2) 第②③行的数与第①行的数分别有什么关系?
(3) 取每行数的第9个数,计算这三个数的和.
答案:
15.解:
(1)-2⁵ 2⁶ -2⁷
(2)第②行的数是由第①行相应的数除以-2得到的;第③行的数是由第①行相应的数加1得到的.
(3)2⁹+2⁹÷(-2)+2⁹+1=512+(-256)+512+1=769.
(1)-2⁵ 2⁶ -2⁷
(2)第②行的数是由第①行相应的数除以-2得到的;第③行的数是由第①行相应的数加1得到的.
(3)2⁹+2⁹÷(-2)+2⁹+1=512+(-256)+512+1=769.
查看更多完整答案,请扫码查看


