《2025年名校课堂七年级数学上册人教版江西专版》

1. (1)数轴上表示 $5$ 的点到原点的距离是5，所以 $|5|=$5；数轴上表示 $-5$ 的点到原点的距离是5，所以 $|-5|=$5；数轴上表示 $0$ 的点到原点的距离是0，所以 $|0|=$0。
(2)$|-2025|$ 的几何意义是数轴上表示-2025的点到原点的距离。

答案： 1.
(1)5 5 5 5 0 0
(2)-2025 原点

2. 已知数轴的负半轴上某一点表示的数的绝对值为 $14$，则这个点表示的数为-14。

答案： 2.-14

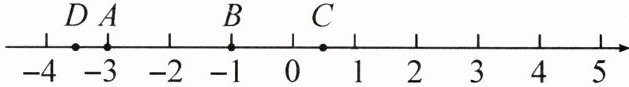
3. 如图，数轴上的点 $A,B,C,D$ 分别表示有理数 $a,b,c,d$，这四个数中，a的绝对值等于 $3$，c的绝对值最小，d的绝对值最大。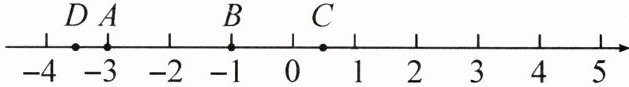

答案： 3.a c d

4. (2024·兰州)$2024$ 的绝对值是(B)

A.$-2024$
B.$2024$
C.$\frac{1}{2024}$
D.$-\frac{1}{2024}$

答案： 4.B

5. (2023·陕西)计算：$|-17|=$(A)

A.$17$
B.$-17$
C.$\frac{1}{17}$
D.$-\frac{1}{17}$

答案： 5.A

6. (2024·大庆)下列各组数中，互为相反数的是(A)

A.$|-2024|$ 和 $-2024$
B.$2024$ 和 $\frac{1}{2024}$
C.$|-2024|$ 和 $2024$
D.$-2024$ 和 $\frac{1}{2024}$

答案： 6.A

7. 已知 $a = -2,b = 1$，则 $|a|+|-b|$ 的值为3。

答案： 7.3

8. 求下列各数的绝对值：
（1）$+\frac{7}{2}$。
（2）$-7.2$。
（3）$-(+1000)$。
（4）$-(-8\frac{1}{3})$。

答案： 8.解:
(1)$|+\frac {7}{2}|=\frac {7}{2}$.
(2)$|-7.2|=7.2$.
(3)$|-(+1000)|=1000$.
(4)$|-(-8\frac {1}{3})|=8\frac {1}{3}.$

9. 化简下列各数：
（1）$+|-\frac{2}{3}|$。
（2）$-|+2.85|$。
（3）$-|-\frac{5}{4}|$。
（4）$|-(-10)|$。

答案： 9.解:
(1)原式$=\frac {2}{3}$.
(2)原式$=-2.85$.
(3)原式$=-\frac {5}{4}$.
(4)原式$=10.$

10. (1)①正数：$|+5|=$5，$|12|=$12。
②负数：$|-7|=$7，$|-15|=$15。
③$0$：$|0|=$0。
(2)根据(1)中的规律发现：不论正数、负数和 $0$，它们的绝对值一定是非负数。

答案： 10.
(1)①5 12 ②7 15 ③0
(2)非负数

11. (2024·威海)一批食品，标准质量为每袋 $454g$。现随机抽取 $4$ 袋样品进行检测，把超过标准质量的克数用正数表示，不足的克数用负数表示。那么，最接近标准质量的是(C)

A.$+7$
B.$-5$
C.$-3$
D.$10$

答案： 11.C

12. 若一个数的绝对值等于 $3$，则这个数是±3。

答案： 12.±3

13. 如果 $|x| = |-5|$，那么 $x=$±5。

答案： 13.±5