第71页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
10. 若 $ m + n = 7 $,$ 2n - p = 4 $,则 $ m - (-3n + p) = $
11
.
答案:
11
11. 已知 $ a $,$ b $ 两数在数轴上的对应点的位置如图所示,则化简 $ |b - a| + |a + b| $ 的结果是
 (题中数轴图)
(题中数轴图)
-2
. (题中数轴图)
(题中数轴图)
答案:
-2
12. 若 $ A $ 是关于 $ x $ 的五次多项式,$ B $ 是关于 $ x $ 的三次多项式,则 $ A + B $ 是(
A.三次多项式
B.五次单项式或多项式
C.八次多项式
D.八次单项式或多项式
B
)A.三次多项式
B.五次单项式或多项式
C.八次多项式
D.八次单项式或多项式
答案:
B
13. 如图,小明想把一张长为 $ a $,宽为 $ b $ 的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形纸片的四个角各剪去一个边长为 $ x $ 的小正方形,用代数式表示纸片剩余部分的周长为(
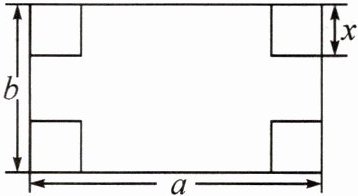
A.$ ab - 4x^{2} $
B.$ 2a + 2b - 8x $
C.$ 2a + 2b - 16x $
D.$ 2a + 2b $
D
)
A.$ ab - 4x^{2} $
B.$ 2a + 2b - 8x $
C.$ 2a + 2b - 16x $
D.$ 2a + 2b $
答案:
D
14. 湖南师大附中校本经典题 已知 $ x $ 为绝对值等于 $ 4 $ 的负数,$ y $ 为最小的正整数,$ z $ 的倒数为 $ -0.5 $ 的相反数,求代数式 $ 4x^{2}y^{3} - [2xyz + (5x^{2}y^{3} - 7xyz) - x^{2}y^{3}] $ 的值.
答案:
解:
∵x为绝对值等于4的负数,y为最小的正整数,z的倒数为-0.5的相反数,
∴$x=-4,y=1,z=2$.
∴原式$=4x^{2}y^{3}-(2xyz+5x^{2}y^{3}-7xyz-x^{2}y^{3})=4x^{2}y^{3}-2xyz-5x^{2}y^{3}+7xyz+x^{2}y^{3}=5xyz=5×(-4)×1×2=-40.$
∵x为绝对值等于4的负数,y为最小的正整数,z的倒数为-0.5的相反数,
∴$x=-4,y=1,z=2$.
∴原式$=4x^{2}y^{3}-(2xyz+5x^{2}y^{3}-7xyz-x^{2}y^{3})=4x^{2}y^{3}-2xyz-5x^{2}y^{3}+7xyz+x^{2}y^{3}=5xyz=5×(-4)×1×2=-40.$
15. 小明的妈妈从菜市场买回 $ 3 $ 千克萝卜、$ 2 $ 千克排骨,准备做萝卜排骨汤. 下面是爸爸妈妈的对话:
妈妈:“上个月萝卜的单价是 $ a $ 元,排骨的单价比萝卜的 $ 7 $ 倍还多 $ 2 $ 元.”
爸爸:“今天新闻上说,与上个月相比,萝卜的单价上涨了 $ 25\% $,排骨的单价上涨了 $ 20\% $.”
请根据上面的对话信息回答下列问题:
(1) 请用含 $ a $ 的代数式填空:上个月排骨的单价是
(2) 小明的妈妈今天买的萝卜和排骨比上月买相同质量的萝卜和排骨一共多花了多少元(列式并化简)?
(3) 当 $ a = 5 $ 时,今天买的萝卜和排骨比上月买相同质量的萝卜和排骨一共多花了多少元(结果保留小数点后一位)?
妈妈:“上个月萝卜的单价是 $ a $ 元,排骨的单价比萝卜的 $ 7 $ 倍还多 $ 2 $ 元.”
爸爸:“今天新闻上说,与上个月相比,萝卜的单价上涨了 $ 25\% $,排骨的单价上涨了 $ 20\% $.”
请根据上面的对话信息回答下列问题:
(1) 请用含 $ a $ 的代数式填空:上个月排骨的单价是
(7a + 2)
元,这个月萝卜的单价是1.25a
元,这个月排骨的单价是(8.4a + 2.4)
元.(2) 小明的妈妈今天买的萝卜和排骨比上月买相同质量的萝卜和排骨一共多花了多少元(列式并化简)?
(3) 当 $ a = 5 $ 时,今天买的萝卜和排骨比上月买相同质量的萝卜和排骨一共多花了多少元(结果保留小数点后一位)?
答案:
解:
(1)$(7a+2)$ $1.25a$ $(8.4a+2.4)$
(2)$3×1.25a+2(8.4a+2.4)-[3a+2(7a+2)]=3.75a+16.8a+4.8-17a-4=3.55a+0.8$.
答:一共花了$(3.55a+0.8)$元.
(3)当$a=5$时,$3.55a+0.8=3.55×5+0.8\approx 18.6$.
答:一共花了约18.6元.
(1)$(7a+2)$ $1.25a$ $(8.4a+2.4)$
(2)$3×1.25a+2(8.4a+2.4)-[3a+2(7a+2)]=3.75a+16.8a+4.8-17a-4=3.55a+0.8$.
答:一共花了$(3.55a+0.8)$元.
(3)当$a=5$时,$3.55a+0.8=3.55×5+0.8\approx 18.6$.
答:一共花了约18.6元.
16. 新考向 阅读理解 阅读材料,并回答下列问题.
对称式:一个含有多个字母的代数式中,如果任意交换两个字母的位置,代数式的值都不变,那么这样的代数式就叫作对称式. 例如:代数式 $ abc $ 中任意两个字母交换位置,可得到代数式 $ bac $,$ acb $,$ cba $. $ \because abc = bac = acb = cba $,$ \therefore abc $ 是对称式;而代数式 $ a - b $ 中字母 $ a $,$ b $ 交换位置,得到代数式 $ b - a $,$ \because a - b \neq b - a $,$ \therefore a - b $ 不是对称式.
(1) 下列四个代数式中,是对称式的是
① $ a + b + c $;② $ a^{2}b $;③ $ a^{2} + b^{2} $;④ $ \frac{a}{b} $.
(2) 写出一个只含有字母 $ m $,$ n $ 的单项式,使该单项式是对称式,且次数为 $ 6 $.
(3) 已知 $ A = 3a^{2} + 6b^{2} $,$ B = a^{2} - 2ab $,求 $ A + 3B $,并直接判断所得结果是否为对称式.
对称式:一个含有多个字母的代数式中,如果任意交换两个字母的位置,代数式的值都不变,那么这样的代数式就叫作对称式. 例如:代数式 $ abc $ 中任意两个字母交换位置,可得到代数式 $ bac $,$ acb $,$ cba $. $ \because abc = bac = acb = cba $,$ \therefore abc $ 是对称式;而代数式 $ a - b $ 中字母 $ a $,$ b $ 交换位置,得到代数式 $ b - a $,$ \because a - b \neq b - a $,$ \therefore a - b $ 不是对称式.
(1) 下列四个代数式中,是对称式的是
②③
(填序号).① $ a + b + c $;② $ a^{2}b $;③ $ a^{2} + b^{2} $;④ $ \frac{a}{b} $.
(2) 写出一个只含有字母 $ m $,$ n $ 的单项式,使该单项式是对称式,且次数为 $ 6 $.
(3) 已知 $ A = 3a^{2} + 6b^{2} $,$ B = a^{2} - 2ab $,求 $ A + 3B $,并直接判断所得结果是否为对称式.
答案:
解:
(1)②③
(2)满足条件的单项式为$m^{3}n^{3}$(答案不唯一).
(3)
∵$A=3a^{2}+6b^{2},B=a^{2}-2ab$,
∴$A+3B=3a^{2}+6b^{2}+3(a^{2}-2ab)=3a^{2}+6b^{2}+3a^{2}-6ab=6a^{2}+6b^{2}-6ab$.
∵$6a^{2}+6b^{2}-6ab=6b^{2}+6a^{2}-6ba$,
∴$A+3B$的结果是对称式.
(1)②③
(2)满足条件的单项式为$m^{3}n^{3}$(答案不唯一).
(3)
∵$A=3a^{2}+6b^{2},B=a^{2}-2ab$,
∴$A+3B=3a^{2}+6b^{2}+3(a^{2}-2ab)=3a^{2}+6b^{2}+3a^{2}-6ab=6a^{2}+6b^{2}-6ab$.
∵$6a^{2}+6b^{2}-6ab=6b^{2}+6a^{2}-6ba$,
∴$A+3B$的结果是对称式.
查看更多完整答案,请扫码查看


