第17页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
16. (2024·南充期末)已知 |m - 2| = 0,则 m 的值为
2
.
答案:
2
17. 若 |a| = 1,|b| = 5,且 a > b,则 a =
±1
,b = -5
.
答案:
±1 -5
18. 绝对值不大于 2 的所有整数为
0 ±1,±2
.
答案:
0 ±1,±2
19. 新考向 真实情境 某汽车配件厂生产一批圆形零件,从中抽取 5 件样品进行检验,比标准直径长的毫米数记作正数,比标准直径短的毫米数记作负数,检查记录如下:
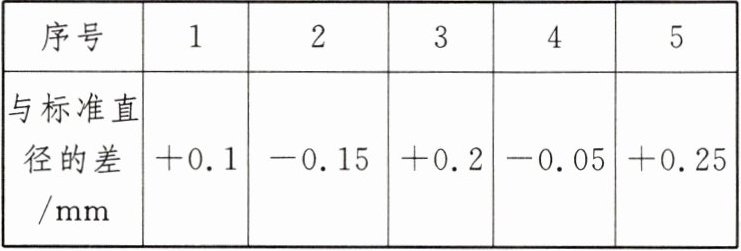
(1) 哪件样品的质量相对好一些?用绝对值的知识进行说明.
(2) 若规定与标准直径的误差不超过 0.18 mm 的是合格产品,超过 0.18 mm 但不超过 0.22 mm 的是次品,超过 0.22 mm 的是废品,则这 5 件样品分别属于哪类产品?说明理由.

(1) 哪件样品的质量相对好一些?用绝对值的知识进行说明.
(2) 若规定与标准直径的误差不超过 0.18 mm 的是合格产品,超过 0.18 mm 但不超过 0.22 mm 的是次品,超过 0.22 mm 的是废品,则这 5 件样品分别属于哪类产品?说明理由.
答案:
(1) 各样品与标准直径差值的绝对值分别为:
$|+0.1| = 0.1$,
$|-0.15| = 0.15$,
$|+0.2| = 0.2$,
$|-0.05| = 0.05$,
$|+0.25| = 0.25$。
由于$0.05 \lt 0.1 \lt 0.15 \lt 0.2 \lt 0.25$,
第4件样品的绝对值最小,所以第4件样品的质量相对好一些。
(2) 根据误差规定:
$|+0.1| = 0.1 \lt 0.18$,第1件是合格产品;
$|-0.15| = 0.15 \lt 0.18$,第2件是合格产品;
$|+0.2| = 0.2$,$0.18 \lt 0.2 \lt 0.22$,第3件是次品;
$|-0.05| = 0.05 \lt 0.18$,第4件是合格产品;
$|+0.25| = 0.25 \gt 0.22$,第5件是废品。
综上,第1、2、4件是合格产品,第3件是次品,第5件是废品。
(1) 各样品与标准直径差值的绝对值分别为:
$|+0.1| = 0.1$,
$|-0.15| = 0.15$,
$|+0.2| = 0.2$,
$|-0.05| = 0.05$,
$|+0.25| = 0.25$。
由于$0.05 \lt 0.1 \lt 0.15 \lt 0.2 \lt 0.25$,
第4件样品的绝对值最小,所以第4件样品的质量相对好一些。
(2) 根据误差规定:
$|+0.1| = 0.1 \lt 0.18$,第1件是合格产品;
$|-0.15| = 0.15 \lt 0.18$,第2件是合格产品;
$|+0.2| = 0.2$,$0.18 \lt 0.2 \lt 0.22$,第3件是次品;
$|-0.05| = 0.05 \lt 0.18$,第4件是合格产品;
$|+0.25| = 0.25 \gt 0.22$,第5件是废品。
综上,第1、2、4件是合格产品,第3件是次品,第5件是废品。
20. 在 -0.25,+2.3,0,-$\frac{3}{2}$这四个数中,最小的数是(
A.-0.25
B.+2.3
C.0
D.-$\frac{3}{2}$
D
)A.-0.25
B.+2.3
C.0
D.-$\frac{3}{2}$
答案:
D
21. 下列有理数的大小关系正确的是(
A.-$\frac{3}{2}$ < -1.25
B.|+6| > |-6|
C.-|-3| > 0
D.-(-$\frac{1}{3}$) < -|-$\frac{1}{4}$|
A
)A.-$\frac{3}{2}$ < -1.25
B.|+6| > |-6|
C.-|-3| > 0
D.-(-$\frac{1}{3}$) < -|-$\frac{1}{4}$|
答案:
A
22. 把下列各数表示在数轴上,然后把这些数按从小到大的顺序用“<”连接起来.
0,1$\frac{1}{2}$,-3,-(-0.5),-|-$\frac{3}{4}$|,+( -4$\frac{1}{3}$).
 ]
]
0,1$\frac{1}{2}$,-3,-(-0.5),-|-$\frac{3}{4}$|,+( -4$\frac{1}{3}$).
 ]
]
答案:

+( -4$\frac{1}{3}$) 在 -5 和 -4 之间,标在 -4 附近偏左;
-3 在 -3 位置;
-|-$\frac{3}{4}$| 在 0 左侧,接近 0;
-(-0.5) 即 0.5,在 0 右侧接近 0;
0 在 0 位置;
1$\frac{1}{2}$ 在 1 和 2 中间。
按从小到大的顺序用“<”连接:
+( -4$\frac{1}{3}$)< -3 < -|-$\frac{3}{4}$| < 0 < -(-0.5) < 1$\frac{1}{2}$。
+( -4$\frac{1}{3}$) 在 -5 和 -4 之间,标在 -4 附近偏左;
-3 在 -3 位置;
-|-$\frac{3}{4}$| 在 0 左侧,接近 0;
-(-0.5) 即 0.5,在 0 右侧接近 0;
0 在 0 位置;
1$\frac{1}{2}$ 在 1 和 2 中间。
按从小到大的顺序用“<”连接:
+( -4$\frac{1}{3}$)< -3 < -|-$\frac{3}{4}$| < 0 < -(-0.5) < 1$\frac{1}{2}$。
23. 如图,在一张透明的纸上画一条数轴,点 A,B 在数轴上表示的数分别为 -19,6,以点 C 为折点,将此数轴向右对折. 若对折后点 A 的对应点 A' 落在数轴上,且 A',B 两点之间的距离为 3,则点 C 表示的数是
 ]
]
-8或-5
. ]
]
答案:
-8或-5
24. 新考向 数学文化 1 700 多年前,我国数学家刘徽首次明确地提出了正数和负数的概念. 他还规定筹算时“正算赤,负算黑”,即用红色算筹表示正数,黑色算筹表示负数. 例如:
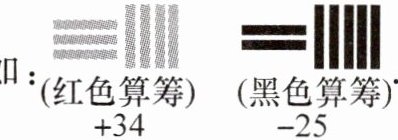
这个记载比国外早了差不多八百年. 根据上述材料,解决问题:
(1) 黑色算筹 表示的有理数是
表示的有理数是
(2) 下列选项所示的算筹中,表示 -35 的是(

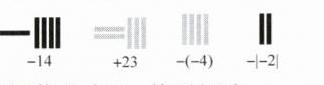
(3) 请画算筹表示下列数:
-14,+23,-(-4),-| -2 |.

这个记载比国外早了差不多八百年. 根据上述材料,解决问题:
(1) 黑色算筹
 表示的有理数是
表示的有理数是-23
.(2) 下列选项所示的算筹中,表示 -35 的是(
A
)
(3) 请画算筹表示下列数:
-14,+23,-(-4),-| -2 |.
答案:
(1)-23
(2)A
(3)
(1)-23
(2)A
(3)

查看更多完整答案,请扫码查看


