《2025年拔尖特训九年级物理上册苏科版》

5.(2023·株洲)投出的铅球在空中飞行,它在整个运动过程中的动能E_k与距离地面的高度h的关系如图所示。已知铅球脱手的高度h为2 m,铅球落到地面时重力势能为零,不计空气阻力,由图可知,铅球脱手时其重力势能为( )

A.80 J
B.100 J
C.180 J
D.280 J

答案： A 解析:由题可知,因为不计空气阻力,机械能守恒,铅球运动过程中只有重力势能和动能的相互转化,若铅球落到地面时重力势能为零,则此时动能取最大值,为280J,此时机械能为280J。由图可知,当铅球到最高点时,即距离地面2.5m时,动能为180J,则重力势能为$E_{p1}=280\ J-180\ J=100\ J=2.5\ m\cdot mg$;已知铅球脱手的高度为2m,所以其重力势能$E_{p2}=2\ m\cdot mg=80\ J$。

6.体育课上,小明在同一位置用相同的力多次将足球踢出,发现足球斜向上飞出的角度越大,球运动得越高,但并不能运动得越远。小明查阅资料后知道：足球所做的运动叫作斜抛运动,其运动轨迹如图甲所示。足球初始运动方向与水平方向的夹角叫作抛射角,抛出点到落地点的水平距离叫作射程,射程与抛出速度和抛射角的大小有关。若物体的动能大小$E_k= \frac{1}{2}mv^2,$重力势能大小E_p= mgh,不计空气阻力,g取10 N/kg,请回答下列问题：
(1)若质量为0.4 kg的足球从地面被踢出时,具有的动能是120 J,被踢出后足球能达到的最大高度是5 m,则足球在最高点时具有的动能是______。
(2)若足球的射程x与抛出速度v、抛射角θ之间满足公式$x= \frac{2v^2\sin\theta\cos\theta}{g},$当足球以20 m/s且与水平方向成45°角的速度被踢出时,足球的射程是______。
(3)足球运动的速度v可以分解成水平方向的速度v_x和竖直方向的速度v_y,三者可构成如图乙所示的矩形。足球在空中飞行时,水平方向的速度保持不变,竖直方向的速度先减小后增大。若足球在地面以$10\sqrt{2} m/s$且与水平方向成45°角的速度被踢出,当足球的速度与水平方向的夹角为30°时,足球距地面的高度约为______m。(结果保留两位小数)

答案： （1）100J （2）40m （3）3.33 解析:（1）取地面为零势能面,从地面被踢出时足球具有的动能$E_{k1}=120\ J$,具有的重力势能$E_{p1}=0$,足球被踢出后能达到的最大高度是5m,具有的重力势能$E_{p2}=mgh=0.4\ kg× 10\ N/kg× 5\ m=20\ J$,因不计空气阻力时足球的机械能守恒,所以,有$E_{1}=E_{2}$,即$E_{k1}+E_{p1}=E_{k2}+E_{p2}$,则足球在最高点时具有的动能$E_{k2}=E_{k1}+E_{p1}-E_{p2}=120\ J+0-20\ J=100\ J$。（2）当足球以20m/s且与水平方向成$45^{\circ}$角的速度被踢出时,足球的射程$x=\frac{2v^{2}\sin\theta \cos\theta }{g}=\frac{2× (20\ m/s)^{2}× \frac{\sqrt{2}}{2}× \frac{\sqrt{2}}{2}}{10\ N/kg}=40\ m$。（3）若足球在地面以$10\sqrt{2}\ m/s$且与水平方向成$45^{\circ}$角的速度被踢出,则水平方向的速度$v_{x}=v'\cos45^{\circ}=10\sqrt{2}\ m/s× \frac{\sqrt{2}}{2}=10\ m/s$,因足球在空中飞行时,水平方向的速度保持不变,所以,当足球的速度与水平方向的夹角为$30^{\circ}$时,足球的速度$v''=\frac{v_{x}}{\cos30^{\circ}}=\frac{10\ m/s}{\frac{\sqrt{3}}{2}}=\frac{20\sqrt{3}}{3}\ m/s$,因不计空气阻力时足球的机械能守恒,所以,有$E_{k1}'+E_{p1}'=E_{k2}'+E_{p2}'$,即$\frac{1}{2}mv'^{2}+0=\frac{1}{2}mv''^{2}+mgh'$,此时足球距地面的高度$h'=\frac{v'^{2}-v''^{2}}{2g}=\frac{(10\sqrt{2}\ m/s)^{2}-(\frac{20\sqrt{3}}{3}\ m/s)^{2}}{2× 10\ N/kg}=\frac{10}{3}\ m\approx 3.33\ m$。

7.已知物体的重力势能表达式为E_p= mgh,动能表达式为$E_k= \frac{1}{2}mv^2；$其中m为物体的质量,h为物体距离水平地面的高度,v为物体的运动速度,g取10 N/kg,取地面为零势能面。如图所示,将一质量为0.4 kg的物体从距离地面1.5 m的高度沿水平方向以2 m/s的速度抛出。不计空气阻力,物体从被抛出到落地的瞬间,整个过程中机械能守恒。求：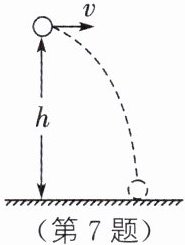
(1)物体被抛出时的重力势能E_p和动能E_k1。
(2)物体从被抛出至落地的过程中,其重力所做的功W。
(3)物体落地前瞬间的动能E_k2。

答案： （1）物体被抛出时的重力势能$E_{p}=mgh=0.4\ kg× 10\ N/kg× 1.5\ m=6\ J$;动能$E_{k1}=\frac{1}{2}mv^{2}=\frac{1}{2}× 0.4\ kg× (2\ m/s)^{2}=0.8\ J$（2）物体从被抛出至落地的过程中,其重力所做的功$W=Gh=mgh=0.4\ kg× 10\ N/kg× 1.5\ m=6\ J$（3）物体下落时高度减小,速度增大,所以重力势能转化为动能,落地时高度为0,重力势能全部转化为动能,所以物体落地前瞬间的动能$E_{k2}=E_{k1}+E_{p}=0.8\ J+6\ J=6.8\ J$