《2025年拔尖特训九年级物理上册苏科版》

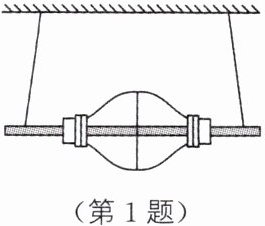
1.(2024·临夏)某科技兴趣小组取两个瓶子,从瓶口以下约6 cm处截断,将截断处用胶水黏合在一起,再从瓶口的橡胶塞中心穿一根长约20 cm的细木棒,用两条悬线拴住木棒的两端,将悬线固定在支架上,就得到了如图所示的滚摆。在滚摆从上到下运动的过程中,重力势能主要转化为______能；滚摆每次上升的高度逐渐减小,说明滚摆的机械能______(变大/不变/变小)。

答案： 动 变小

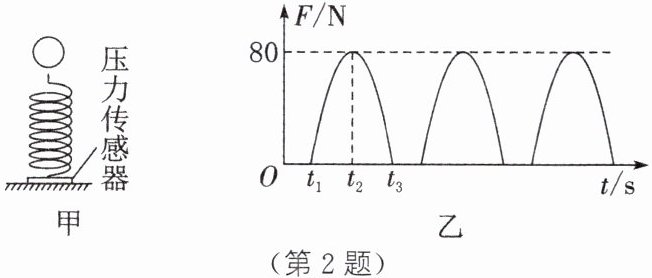
2.如图甲所示,质量忽略不计的弹簧竖直固定在水平面上,t= 0时刻,将一重力G= 50 N的金属小球从弹簧正上方某一高度处由静止释放,小球落到弹簧上并压缩弹簧到最低点,然后又被弹起而离开弹簧,上升到一定高度后再下落,如此反复,通过安装在弹簧下端的压力传感器,测出这一过程中弹簧弹力F随时间t变化的图像如图乙所示,则在上述过程中,t1时刻小球的动能______(是/不是)最大的；小球在从最高点到最低点的运动过程中,动能的变化情况是______；t2～t3时间段内,小球增加的动能______(大于/等于/小于)弹簧减少的弹性势能,上述过程中小球和弹簧总的机械能______(是/不是)守恒的。

答案： 不是 先变大后变小 小于 是 解析:小球从最高点下落到与弹簧刚接触的阶段,重力势能转化为动能,动能增大;由图乙知,$t_{1}$时刻弹力$F=0$,此时小球刚接触弹簧,$t_{2}$时刻弹力$F$达到最大值80N,此时弹簧发生的形变最大,小球到达最低点;$t_{1}\sim t_{2}$时间段内,弹力$F$逐渐增大,在$F$未增大到50N阶段,$G＞F$,小球加速向下,小球的动能增大,当$F=50N$时,$F=G$,小球的速度最大,动能最大,此后由于$F＞G$,小球减速向下,小球的动能减小,由上述分析可知,$t_{1}$时刻小球的动能不是最大的,小球从最高点到最低点的运动过程中,动能的变化情况是先变大后变小。由图乙知,$t_{3}$时刻弹力$F=0$,此时弹簧刚好恢复原状,$t_{2}\sim t_{3}$时间段内,弹簧的弹性势能转化为小球的动能和重力势能。小球增加的动能小于弹簧减少的弹性势能。由图乙知,小球上下运动的过程中每次弹力达到最大值都相等,说明小球和弹簧总的机械能守恒。

3.某手机软件具有录音和显示波形的功能。某乒乓球爱好者将一乒乓球从一定高度由静止释放,利用该手机软件记录下乒乓球碰撞台面时发出的声音,其波形随时间的变化如图所示。下列说法中,正确的是( )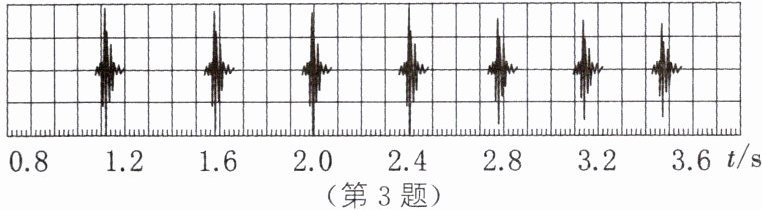

A.每次发声的时间间隔相等
B.整个过程中乒乓球的机械能不变
C.乒乓球每次弹起时的动能依次减小
D.乒乓球每次与台面碰撞的最大形变程度相同

答案： C 解析:由图可以看出每次发声的时间间隔不相等,A错误;每次发声的时间间隔不相等,说明乒乓球上升的高度越来越小,整个过程中乒乓球的机械能变小,B错误;乒乓球的机械能越来越小,则乒乓球每次弹起时的动能依次减小,乒乓球每次与台面碰撞时的弹性势能越来越小,故最大形变程度越来越小,C正确,D错误。

4.小丽在探究“弹簧弹力大小与形变量的关系”时,发现同一根弹簧的弹力大小F与形变量$\Delta x$的比值k恒定。现小丽有两根原长相等的弹簧1和2,已知k1:k2= 1:2,在两根弹簧下分别挂同一物体,静止时弹簧1和2的伸长量分别为$\Delta x1和\Delta x2,则\Delta x1:\Delta x2= ______。小丽通过查阅资料知道弹簧的弹性势能E_p= \frac{1}{2}k\Delta x^2,$此时弹簧1和2的弹性势能分别为E_p1和E_p2,则E_p1:E_p2= ______。小丽将弹簧1和2同时用来悬挂一物体,静止时如图甲所示,两弹簧的弹性势能之和为E_p甲。将弹簧1和2连接后用来悬挂同一物体,静止时如图乙所示,两弹簧的弹性势能之和为E_p乙,则E_p甲:E_p乙= ______。(已知图甲情况下悬挂物体时弹簧1和2伸长量相同,整个实验中弹簧所受重力不计,且均处于弹性限度内)

答案： $2:1$$2:1$$2:9$解析:在弹簧下悬挂物体,静止时,物体受到的弹力$F$与重力$G$二力平衡,$F=G$,据题有$F_{1}''=F_{2}''$,由$F=k\Delta x$可得$\Delta x=\frac{F}{k}$,$\Delta x_{1}=\frac{F_{1}''}{k_{1}}$,$\Delta x_{2}=\frac{F_{2}''}{k_{2}}$,则$\frac{\Delta x_{1}}{\Delta x_{2}}=\frac{F_{1}''}{F_{2}''}× \frac{k_{2}}{k_{1}}=2:1$,由$E_{p}=\frac{1}{2}k\Delta x^{2}$可得$\frac{E_{p1}}{E_{p2}}=\frac{k_{1}}{k_{2}}× (\frac{\Delta x_{1}}{\Delta x_{2}})^{2}=\frac{2}{1}× (\frac{2}{1})^{2}=8:1$。设如图甲所示的情况下,弹簧1、2的伸长量均为$\Delta x$,则$\frac{F_{1}}{F_{2}}=\frac{k_{1}\Delta x}{k_{2}\Delta x}=\frac{1}{2}$,$F_{1}=\frac{1}{2}F_{2}$①,据力的平衡条件有$F_{1}+F_{2}=G_{物}$②,由①②可得有$F_{1}=\frac{1}{3}G_{物}$③,$F_{2}=\frac{2}{3}G_{物}$④,$E_{p甲}=\frac{1}{2}k_{1}\Delta x^{2}+\frac{1}{2}k_{2}\Delta x^{2}=\frac{3}{2}k_{1}\Delta x^{2}$⑤。如图乙所示的情况下,据力的平衡条件和题意有$F_{1}'=G_{物}$⑥,$F_{2}'=G_{物}$⑦,由$F=k\Delta x$和③⑥可知,$\Delta x_{1}'=3\Delta x$;由$F=k\Delta x$和④⑦可知,$\Delta x_{2}'=\frac{3}{2}\Delta x$,$E_{p乙}=\frac{1}{2}k_{1}× (3\Delta x)^{2}+\frac{1}{2}k_{2}× (\frac{3}{2}\Delta x)^{2}=\frac{27}{4}k_{1}\Delta x^{2}$⑧,由⑤⑧可得$\frac{E_{p甲}}{E_{p乙}}=2:9$。本题后两空的另一种解法:因为弹簧所获得的弹性势能等于所挂重物的重力做的功,所以$\frac{E_{p1}}{E_{p2}}=\frac{G\Delta x_{1}}{G\Delta x_{2}}=2:1$;设如图甲所示的情况下,弹簧1、2的伸长量均为$\Delta x_{甲}$,则如图乙所示的情况下,弹簧1、2的总伸长量$\Delta x_{乙}=3\Delta x_{甲}+\frac{3}{2}\Delta x_{甲}=\frac{9}{2}\Delta x_{甲}$,$\frac{E_{p甲}}{E_{p乙}}=\frac{G\Delta x_{甲}}{G\Delta x_{乙}}=2:9$。