《2025年拔尖特训九年级物理上册苏科版》

1. 新情境·古代科技(2024·无锡)如图所示为《天工开物》记载的我国古代的提水工具“辘轳”,在两个支架 答案讲解 上摆放一根直的硬棒,支点为$O_1$、$O_2$,A点系一石块,B点装有轮轴,轮轴能绕着硬棒转动,悬吊空桶的绳索另一端绕过轮轴后系紧在轮轴上。若空桶质量为10 kg,轮轴质量为10 kg,空桶和轮轴对硬棒的作用力视作施加在B点,$O_1A$长为0.6 m,$O_1O_2$长为1 m,$O_2B$长为0.8 m,硬棒及绳索质量忽略不计。(g取10 N/kg)

(1)人对辘轳不施加力,且桶中未装水时,为保证硬棒不会翻转,石块质量最多为______kg；若在A点系上质量为40 kg的石块,提水时为保证硬棒不翻转,桶中最多可装______kg的水。
(2)若桶内水的质量为40 kg,人用时20 s将桶匀速提升3 m,此时辘轳提水的机械效率为50％,则桶对水做的功为______J,人做功的功率为______W。

答案： 1.（1）60 60 （2）1200 120
解析:（1）桶中未装水,A 点系石块,硬棒刚好翻转时支点为$O_{1}$点,由杠杆平衡条件可得,$m_{石块}g×l_{O_{1}A}=$（$m_{桶}+m_{轮}$）$g×l_{O_{1}B}$,即$m_{石块}×$0.6m=（10kg+10kg）×（1m+0.8m）,解得$m_{石块}=60kg$;若A 点系上质量为40 kg 的石块,桶中装水,硬棒刚好翻转时支点为$O_{2}$点,由杠杆平衡条件可得,$m_{石}g×l_{O_{2}A}=$（$m_{桶}+$$m_{轮}+m_{水}$）$g×l_{O_{2}B}$,即40kg×（0.6m+1m）=（10kg+10kg+$m_{水}$）×0.8m,解得桶中水的最大质量$m_{水}=60kg$。（2）桶对水做的功$W_{有用}=Gh=m_{水}gh=40kg×10N/kg×$3m=1200J;总功$W_{总}=\frac {W_{有用}}{η}=$$\frac {1200J}{50\% }=2400J$,人做功的功率$P=$$\frac {W_{总}}{t}=\frac {2400J}{20s}=120W$。

2. (2023·荆州)在某场地建设过程中,工人利用长度$s= 3\ m$的斜面把质量为240 kg的重物匀速推到$h= 1\ m$的高处,如图所示,工人所用推力$F= 1000\ N$。g取10 N/kg。
(1)求推力做的有用功。
(2)求斜面的机械效率。
(3)工人将另一质量为300 kg的重物匀速推到同一高度,为了省力,换用长度为5 m的斜面,此时重物与斜面间的摩擦力与原来的摩擦力之比为6∶5,共用时20 s,求工人推力做功的功率。

答案： 2.（1）推力做的有用功$W_{有用}=Gh=$$mgh=240kg×10N/kg×1m=$$2400J$（2）推力做的总功$W_{总}=$$Fs=1000N×3m=3000J$,斜面的机械效率$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {2400J}{3000J}×$$100\% =80\% $（3）此过程中的额外功$W_{额外}=W_{总}-W_{有用}=3000J-$$2400J=600J$,由$W_{额外}=fs$得重物与斜面间的摩擦力$f=\frac {W_{额外}}{s}=$$\frac {600J}{3m}=200N$。工人将另一质量为300kg的重物匀速推到同一高度,为了省力,换用长度为5m的斜面,此时重物与斜面间的摩擦力与原来的摩擦力之比为$6:5$,即$f'=\frac {6}{5}×200N=$$240N$,有用功$W'_{有用}=G'h=m'gh=$$300kg×10N/kg×1m=3000J$;额外功$W'_{额外}=f's'=240N×5m=$$1200J$;则总功$W'_{总}=W'_{有用}+$$W'_{额外}=3000J+1200J=4200J$;推力做功的功率$P=\frac {W'_{总}}{t}=\frac {4200J}{20s}=$$210W$

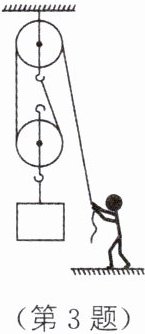
3. 用如图所示的滑轮组将重为300 N的物体以0.1 m/s的速度匀速向上提升10 s。
(1)若不计动滑轮重、绳重和滑轮与轴间的摩擦,求人对绳的拉力$F$。
(2)实际动滑轮重为40 N,人的拉力做功400 J,求滑轮组的机械效率以及克服绳重和摩擦所做的额外功。

答案： 3.（1）由图可知$n=2$,因为不计动滑轮重、绳重和滑轮与轴间的摩擦,所以绳子自由端的拉力$F=\frac {1}{n}G=\frac {1}{2}×$$300N=150N$（2）由$v=\frac {s}{t}$可知,物体上升的高度$h=vt=0.1m/s×$$10s=1m$,拉力做的有用功$W_{有用}=$$Gh=300N×1m=300J$,滑轮组的机械效率$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {300J}{400J}×$$100\% =75\% $;拉力做的额外功$W_{额外}=W_{总}-W_{有用}=400J-300J=$$100J$,克服动滑轮重力做的额外功$W_{动}=G_{动}h=40N×1m=40J$,则克服绳重和摩擦所做的额外功$W=$$W_{额外}-W_{动}=100J-40J=60J$