《2025年拔尖特训九年级数学上册苏科版》

1.(2023·临沂)将一个正六边形绕其中心旋转后仍与原图形重合,旋转角的度数不可能是(B)
A.$60^{\circ}$
B.$90^{\circ}$
C.$180^{\circ}$
D.$360^{\circ}$

答案： B

2.(2024·甘孜)如图,正六边形ABCDEF内接于$\odot O$,$OA= 1$,则AB的长为(C)

A.2
B.$\sqrt{3}$
C.1
D.$\frac{1}{2}$

答案： C

3.(2023·衡阳)用若干个全等的正五边形排成圆环状,如图所示为其中3个正五边形的位置.要完成这一圆环排列,共需要的正五边形的个数是______10.

答案： 10

4.如图所示为$\odot O和\odot O$上的一点A.
(1)作$\odot O$的内接正六边形ABCDEF(保留作图痕迹,无需说明作法).
(2)连接BF、CE.请判断四边形BCEF的形状,并加以证明.

答案：

(1)如图，正六边形ABCDEF即为所求作.
(2)四边形BCEF是矩形. 如图，连接OE.
∵六边形ABCDEF是正六边形，
∴AB=AF=DE=DC=FE=BC.
∴$\overset{\frown}{AB}=\overset{\frown}{AF}=\overset{\frown}{DE}=\overset{\frown}{DC}$.
∴$\overset{\frown}{BF}=\overset{\frown}{CE}$.
∴BF=CE. 又
∵FE=BC,
∴四边形BCEF是平行四边形.
∴∠CEF=∠FBC.
∵四边形BCEF内接于$\odot O$，
∴∠CEF+∠FBC=180°.
∴∠CEF=∠FBC=90°.
∴四边形BCEF是矩形.

5.如图,$\odot O$与正六边形OABCDE的边OA、OE分别交于点F、G,M为$\widehat{FG}$的中点,连接FM、MG.若$FM= 2\sqrt{2}$,则$\odot O$的半径为( )

A.2
B.$\sqrt{6}$
C.$2\sqrt{2}$
D.$2\sqrt{6}$

答案：
C 解析:如图,连接OM.
∵在正六边形OABCDE中,∠FOG=120°,M为$\overset{\frown}{FG}$的中点,
∴∠FOM=60°.
∵OM=OF,
∴△OFM是等边三角形.
∴OM=OF=FM=$2\sqrt{2}$.
∴$\odot O$的半径为$2\sqrt{2}$.

6.(2024·南京玄武期末)如图,在正五边形ABCDE中,连接CE,以点E为圆心、EA长为半径画弧,与CE交于点F,连接AF,则$\angle AFE$的度数是54°.

答案： 54 解析:在正五边形ABCDE中，∠AED=∠CDE=$\frac{(5 - 2)×180^\circ}{5}$ = 108°.
∵DE=CD,
∴∠DCE = ∠CED = $\frac{1}{2}$×(180° - 108°)=36°.
∴∠AEF = 108° - 36° = 72°.
∵AE = EF,
∴∠EAF = ∠AFE = $\frac{1}{2}$×(180° - 72°)=54°.

7.如图,正方形ABCD内接于$\odot O$,E为$\widehat{BC}$上一点,连接BE、CE.若$\angle CBE= 15^{\circ}$,$BE= 5$,则正方形ABCD的边长为______.

答案：
$5\sqrt{2}$ 解析:如图,连接AO、BO、EO.
∵正方形ABCD内接于$\odot O$,
∴OA = OB = OE.
∵∠AOB = $\frac{360^\circ}{4}$ = 90°,AB = BC,∠ABC = 90°,
∴∠OAB = ∠OBA = $\frac{1}{2}$(180° - ∠AOB)=45°.
∴∠OBC = ∠ABC - ∠OBA = 45°.
∵∠CBE = 15°,
∴∠OBE = ∠OBC + ∠CBE = 60°.
∴△OBE是等边三角形.
∴OB = BE = 5.
∴OA = OB = 5.
∴AB = $\sqrt{OA^2 + OB^2}$ = $5\sqrt{2}$.
∴正方形ABCD的边长为$5\sqrt{2}$.

8.新考法·探究题(2024·蚌埠模拟)如图所示分别为正方形、正五边形、正六边形.

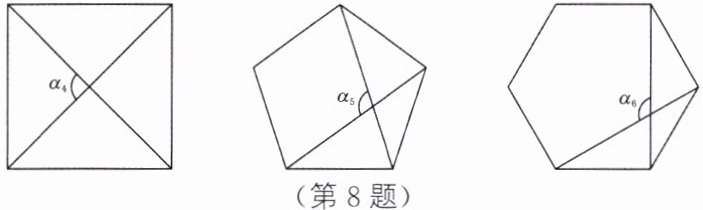
(1)观察图中各正多边形相邻两对角线相交所形成的较大的角$\alpha_{4}$、$\alpha_{5}$、$\alpha_{6}$,则$\alpha_{4}= $90°,$\alpha_{5}= $108°,$\alpha_{6}= $120°.
(2)按此规律,记正n边形相邻两对角线相交所形成的较大的角为$\alpha_{n}$,请用含n的式子表示$\alpha_{n}= $$\frac{(n - 2)\cdot180^\circ}{n}$(其中n为不小于4的整数).
(3)若$\alpha_{n}= 150^{\circ}$,求相应的正多边形的边数n.
∵$a_n=\frac{(n - 2)\cdot180^\circ}{n}$,∴$a_n = 150^\circ=\frac{(n - 2)\cdot180^\circ}{n}$,解得n = 12.

答案：
(1)90;108;120.
(2)$\frac{(n - 2)\cdot180^\circ}{n}$.
(3)
∵$a_n=\frac{(n - 2)\cdot180^\circ}{n}$,
∴$a_n = 150^\circ=\frac{(n - 2)\cdot180^\circ}{n}$,解得n = 12.