《2025年拔尖特训九年级数学上册苏科版》

1. 已知一元二次方程 $3x^2 + 1 = 6x$ 的一次项系数为6,则它的二次项系数和常数项分别为(B)
A.3、1
B.-3、-1
C.3、-1
D.$-3x^2$、-1

答案： B

2. (2024·东莞模拟)如果关于 $x$ 的一元二次方程 $ax^2 + bx + 1 = 0$ 的一个解是 $x = 1$,那么代数式 $2022 - a - b$ 的值为(D)
A.-2022
B.2021
C.2022
D.2023

答案： D

3. (2024·常州天宁期中)若 $(m + 3)x^{|m| - 1} - (m - 3)x - 5 = 0$ 是关于 $x$ 的一元二次方程,则 $m$ 的值为3。

答案： 3 解析:
∵(m+3)x^{|m|-1}-(m-3)x-5=0是关于x的一元二次方程,
∴$\begin{cases} m+3≠0, \\ |m|-1=2, \end{cases}$解得m=3.

4. 若关于 $x$ 的一元二次方程 $(a - 1)x^2 - ax + a^2 = 0$ 的一个根为1,则 $a$ 的值为-1。

答案： -1 解析:把x=1代入(a-1)x²-ax+a²=0中,得a²=1.
∴a=±1.由题意,得a-1≠0,即a≠1.
∴a=-1.

5. 把下列关于 $x$ 的一元二次方程化成一般形式,并写出它的二次项系数、一次项系数和常数项。
(1)$(x - 4)(x + 3) = 15$。
(2)$(x + 5)^2 - 2x(x - 4) = 4x - 3$。
(3)$3x(x - 4) = 2(x - 4)$。
(4)$4(x - 3)^2 = 9(x + 1)^2$。

答案：
(1)x²-x-27=0,它的二次项系数为1,一次项系数为-1,常数项为-27.
(2)-x²+14x+28=0,它的二次项系数为-1,一次项系数为14,常数项为28.
(3)3x²-14x+8=0,它的二次项系数为3,一次项系数为-14,常数项为8.
(4)-5x²-42x+27=0,它的二次项系数为-5,一次项系数为-42,常数项为27.

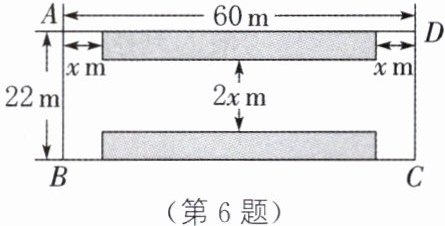
6. (2024·西宁)如图,小区物业计划在一个长60 m、宽22 m的矩形场地 $ABCD$ 上,修建一个小型停车场,涂色部分为停车位所在区域,两侧是宽 $x$ m的道路,中间是宽 $2x$ m的道路。如果涂色部分的总面积是 $600\ m^2$,那么 $x$ 满足的方程是(A)

A.$x^2 - 41x + 180 = 0$
B.$x^2 - 41x + 225 = 0$
C.$x^2 - 41x + 30 = 0$
D.$x^2 - 41x - 270 = 0$

答案： A 解析:
∵矩形场地ABCD的长为60 m,宽为22 m,且停车位的两侧是宽x m的道路,中间是宽2x m的道路,
∴停车位(即涂色部分)可合成长为(60-2x)m、宽为(22-2x)m的矩形.根据题意,得(60-2x)(22-2x)=600,化简,得x²-41x+180=0.

7. 已知关于 $x$ 的一元二次方程 $x^2 + ax + b = 0$ 有一个非零实数根 $-b$,则 $a - b$ 的值为(A)
A.1
B.-1
C.0
D.-2

答案： A 解析:
∵关于x的一元二次方程x²+ax+b=0有一个非零实数根-b,
∴b²-ab+b=0.
∵-b≠0,即b≠0,
∴方程两边同时除以b,得b-a+1=0.
∴a-b=1.

8. *若关于 $x$ 的两个不同的方程 $x^2 + ax + 1 = 0$ 和 $x^2 - x - a = 0$ 恰有一个公共根,则 $a$ 的值为(A)
A.2
B.-3
C.-3 或 2
D.2 或 3

答案： A 解析:
∵关于x的两个不同的方程x²+ax+1=0和x²-x-a=0恰有一个公共根,
∴x²+ax+1=x²-x-a,即(a+1)x+a+1=0.
∵易得a≠-1,
∴a+1≠0.
∴x=-1.
∴x=-1是公共根.把x=-1代入x²+ax+1=0,得1-a+1=0,解得a=2.

9. 若在关于 $x$ 的一元二次方程 $ax^2 - bx + c = 0$ 中,$4a + 2b + c = 0$,则此方程必有一根为x=-2。

答案： x=-2

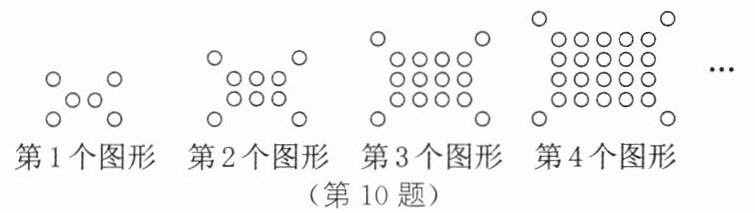
10. 如图所示的图形都由同样大小的小圆圈按一定规律组成的。若按此规律排列下去,第 $n$ 个图形中有160个小圆圈,则可列关于 $n$ 的方程为n²+n+4=160。

答案： n²+n+4=160 解析:观察图形的变化,可知第1个图形中小圆圈的个数为1×2+4=6;第2个图形中小圆圈的个数为2×3+4=10;第3个图形中小圆圈的个数为3×4+4=16;…;
∴第n个图形中小圆圈的个数为n(n+1)+4=n²+n+4.
∵第n个图形中有160个小圆圈,
∴n²+n+4=160.

11. 已知 $m$ 是方程 $x^2 + x - 3 = 0$ 的一个根,则 $m^3 + 2m^2 - 2m + 2024$ 的值为2027。

答案： 2027 解析:
∵m是方程x²+x-3=0的一个根,
∴m²+m-3=0.
∴m²+m=3.
∴m³+2m²-2m+2024=m³+m²+m²-2m+2024=m(m²+m)+m²-2m+2024=3m+m²-2m+2024=m²+m+2024=3+2024=2027.